2025-10-13

Reminder of problem:

Problem Statement: Given a 2-complex $\mathcal{M}\subset [0,1{]}^3$, find a 2-chain in the tetrahedralization of the unit cube $[0,1{]}^3$ that approximates $\mathcal{M}$.

The heuristic approach from 2025-10-10 did not appear to work. Below is an idea for an MIP approach.

Define

• $T$ = set of triangles in the unit cube $[0,1{]}^3$
• $v(t)$ = volume of triangle $t\in T$
• $S$ = set of sample points for $\mathcal{M}$
• $C(s)$ subset of triangles in $T$ that “cover” $s\in S$

We use the following decision variables:

• $x_t\in \{0,1\}$ - triangle $t$ is selected
• $y_s\in \{0,1\}$ - sample $s$ is selected

Objective function:

$$\min \sum _{t\in T}v(t)x_t+\alpha \sum _{s\in S}(1-y_s)$$

To capture $y_s$, we use the following constraint

$$y_s\le \sum _{t\in C(s)}{x}_t\forall s\in S$$

Right now the concern is ensuring that selected triangles are connected. Perhaps we can make use of a dual graph and do network flow?

Define dual graph $G$ where each triangle $t\in T$ is a node and $\{u,v\}\in E$ is an edge if triangles $u$ and $v$ share an edge.

Introduce variable:

• $f_{uv}\ge 0$ - flow from $u$ to $v$

Add two new constraints:

• Flow can only travel along edges if the destination is selected

$$0\le f_{uv}\le M{x}_v\forall \{u,v\}\in E$$

In terms of a choice of $M$, $M=3$ is an apt choice as there is at most 3 edges connecting each vertex.

• Flow conservation

$$\sum _{u\in T}{f}_{uv}-\sum _{u\in T}{f}_{vu}=0$$

Right now there is no incentive for $f_{uv}$ to be positive. We can encourage it by changing the objective to maximize:

$$\max \alpha \sum _{\{u,v\}\in E}{f}_{uv}-\beta \sum _{t\in T}v(t)x_t-\gamma \sum _{s\in S}(1-y_s)$$

Typically in max flow problems, we are sending flow from a source node to a sink node. But in our case, we want the source and sink to be the same triangle.

Final MILP:

$$\begin{array}{rlrlr}& \max & \alpha \sum _{\{u,v\}\in E}{f}_{uv}-\beta \sum _{t\in T}v(t)x_t-\gamma \sum _{s\in S}(1-y_s)& & \\ & \text{s.t.}& y_s\le \sum _{t\in C(s)}{x}_t& & \forall s\in S\\ & & \sum _{u\in T}{f}_{uv}-\sum _{u\in T}{f}_{vu}=0& & \forall v\in T\\ & & 0\le f_{uv}\le 3x_v& & \forall \{u,v\}\in E\\ & & x_t\in \{0,1\}& & \forall t\in T\\ & & y_s\in \{0,1\}& & \forall s\in S\end{array}$$

Of course, this problem is very dependent on choice of parameters.

One thing not yet tackled is how to define $C(s)$, i.e., which triangles “cover” a sample point. Below is a list of ideas on how to define it:

1. Distance based

A sample point $s\in S$ is covered by a triangle $t\in T$ if the distance $d(s,t)$ is less than some threshold value $ϵ$.

2. Containment

A sample point $s\in S$ is covered by a triangle $t\in T$ if $s\in \text{bbox}(t)$.

3. Barycentric coordinates

For each tetrahedron, compute the barycentric coordinates of $s\in S$. $s$ is covered by a triangle if the corresponding ${\lambda }_i$ has $|{\lambda }_i|<ϵ$.

---

Alternative approach is to start with an isosurface $f(x,y,z)=c$ and construct a cube that contains the faces of an isosurface. The idea:

1. Divide the input space into a 3-complex
2. Perform marching tetrahedra to reconstruct the isosurface $f(x,y,z)=c$ as a 2-complex
3. Use the 2-complex to cut the 3-complex for the input space

In other words, this is the new problem statement:

Problem Statement: Given an isosurface $f(\mathbf{x})=c$, construct a 2-chain approximating the isosurface that lies inside a 3-complex.

References:

• https://www.sciencedirect.com/science/article/abs/pii/0167839688900131
• https://ieeexplore.ieee.org/document/885704
• https://ieeexplore.ieee.org/document/1207437
• https://paulbourke.net/geometry/polygonise/

Marching Tetrahedra

We start with describing marching cubes. We divide the space into a 3D grid and sample our function $f(x,y,z)$ for each vertex. For each grid cell, we create planar facets which best represent the isosurface through that grid cell. Using a threshold value, we look for pairs of vertices where one vertex is above the threshold and the other is below. There are 8 vertices of a grid cell, making $8^2=256$ combinations.

We encode each combination with a 8-bit index which is then used to lookup a list of edges (represented by 12-bits) specifying which edges of the cube are cut by the isosurface.

For instance, consider the image below where only vertex 3 is below the isosurface:

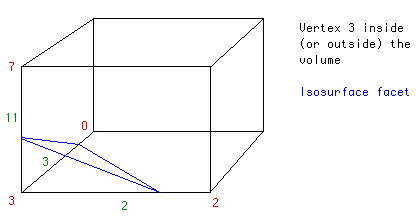
The combination would be given by 0000 1000. Looking up that value in edge table would give 1000 0000 1100 indicating that edges 2, 3 and 11 are cut by the isosurface. The intersection points are calculated by linear interpolation:

$$P=P_1+(\text{isovalue}-f(P_1))(P_2-P_1)/(f(P_2)-f(P_1))$$

where $P_1$ and $P_2$ are the vertices of a cut edge.

We now switch to marching tetrahedra. Each grid cell of our 3-D grid is split into 6 tetrahedrons:

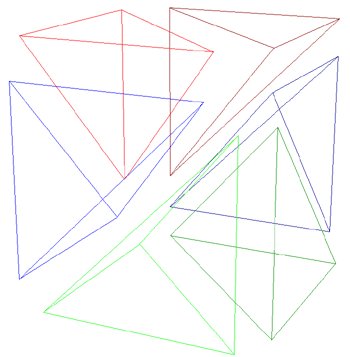
There are now only 4 vertices per tetrahedron. Leaving $4^2=16$ combinations. In other words, due to symmetry, there are only 8 cases for cutting the tetrahedra:

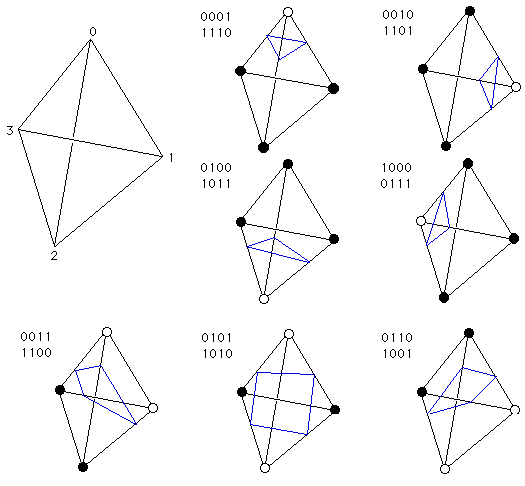
The 8th case (not listed above) is the one where all vertices are above or below the threshold.

Question: Can we pre-cut the tetrahedra so that we can simply mark the corresponding triangles?

Instead of linearly interpolating the points, we weaken the approximation by taking the midpoint. But I am unsure how pre-computing all the cuts would affect the complex. That is, will any of the triangles intersect non-neighboring triangles?

The tetrahedron with the corner cuts (only 1 differing vertex state) looks like the following (a D8 die):

Ignoring the 2 vertex cuts at the moment, the idea would be to replace each tetrahedron with the 4 cut tetrahedra and a tetrahedralization of the above object. Then during the marching process just select the correct faces to be used in the 2-chain.

The two-vertex cuts have the following shape cut out:

The final complex after all cuts is a single tetrahedron. No two non-adjacent of the triangles appear to intersect.

This leaves the following approach:

1. For each tetrahedron in the space do the following:
   1. Subdivide the tetrahedron as described above (unclear on actual implementation of this)
   2. Determine what the combination of vertices (from original tetrahedron) is given by our isosurface $f(x,y,z)=c$.
   3. Lookup which triangles correspond to that combination and mark those triangles as part of the 2-chain.

Going to 4-D should work, except our grid would now be in 4-D resulting in more tetrahedra during the splitting process.