2025-12-15

While using a cubicial complex significantly reduces the number of simplices, the marching cube algorithm is more complex than the marching tetrahedra algorithm. Each tetrahedra in marching tetrahedra correspond to 8 cases. Upto rotation, marching cubes has 15 cases. It is unclear if these cases can be built with cubes.

Below is my attempt to handle each case. I do not think these pieces connect correctly without introducing holes.

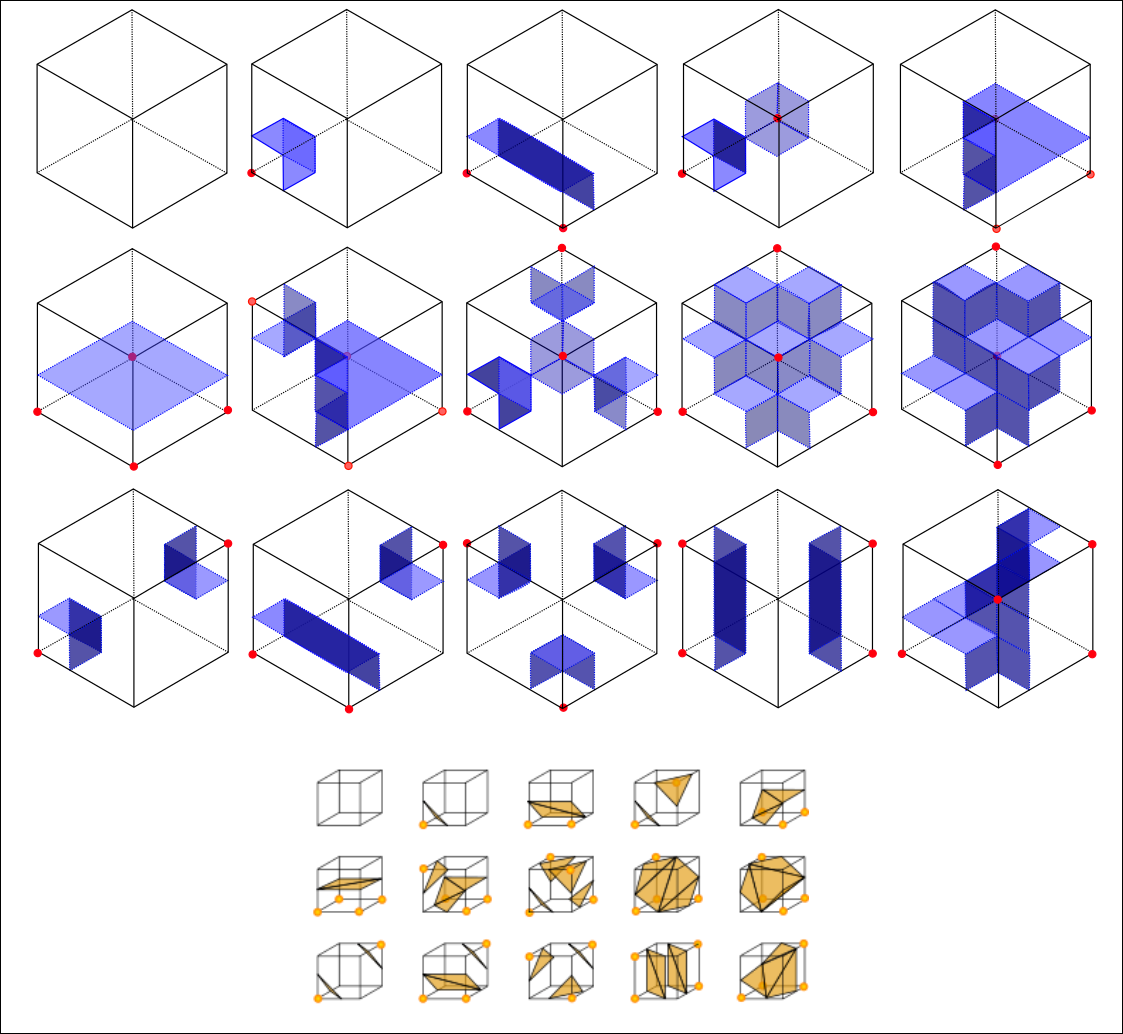
Even if they did, we also need to ensure they connect correctly in 4D.

Potential Fix: Make each case a valid cubicial complex with no holes. When gluing two pieces together, remove any overlapping faces. However, this may introduce unwanted voids into the surface.

New Simpler Approach

We start with a 3D analog. Consider a cubicial complex of a 3D unit cube. Consider two parallel faces:

$$F_1=\{z=0\}\text{ and }{F}_2=\{z=1\}.$$

Define the 1-chain $z={\phi }_1-{\phi }_2$ where

$${\phi }_1=\partial F_1\text{ and }{\phi }_2=\partial F_2.$$

Right now, this instance gives the zero chain. Indeed, let $y=F_2-F_1$. Then

$$\partial y+z=({\phi }_2-{\phi }_1)+({\phi }_1-{\phi }_2)=0.$$

However, if we add some holes this problem is avoided. That is, we add a hole going from the center of $F_1$ to the center of $F_2$.

Lets now extend to 4D. A 4-dimensional cubicial complex with 6 vertices along each axis can be represented by an $11\times 11\times 11\times 11$ array of cells. As an example, below is a 2D example with 5 vertices along the $x$- and $y$-axis (image source):

The dimension of a cell $(x,y,z,w)$ is given by the number of even values (odd if starting from 0) in its coordinate. For instance, $(2,2)$ above would be the square (dimension 2) in the bottom-left corner. The boundary map follows a simple pattern. Consider a square $(x,y)$ in the above array; then the boundary is given by

$$\partial (x,y)=(x+1,y)+(x,y+1)-(x-1,y)-(x,y-1).$$

Consider the faces (dimension 3) given by

$$F_1=\{(x,y,z,1):x,y,z\in \{2,4,6,8,10\}\}\text{ and }{F}_2=\{(x,y,z,11):x,y,z\in \{2,4,6,8,10\}\}$$

which gives the 2-cycles

$$\begin{array}{rl}{\pi }_1& =\partial F_1=\sum _{x,y,z\in \{2,4,6,8,10\}}\sum _{i=1}^3[(x+{\delta }_1(i),y+{\delta }_2(i),z+{\delta }_3(i),1)-(x-{\delta }_1(i),y-{\delta }_2(i),z-{\delta }_3(i),1)]\\ {\pi }_2& =\partial F_2=\sum _{x,y,z\in \{2,4,6,8\}}\sum _{i=1}^3[(x+{\delta }_1(i),y+{\delta }_2(i),z+{\delta }_3(i),11)-(x-{\delta }_1(i),y-{\delta }_2(i),z-{\delta }_3(i),11)].\end{array}$$

Define the input 2-cycle $\pi ={\pi }_1-{\pi }_2$. Right now, this should be homologous to the zero-cycle. However, if cut a hole through our 4D cube (by removing the cells $\{(6,6,6,w):1\le w\le 11\}$) then the optimal cycle should be ${\pi }^{\prime }={\pi }_2^{\prime }-{\pi }_1^{\prime }$ where

$$\begin{array}{rl}{\pi }_1^{\prime }& =\sum _{i=1}^3[(6+{\delta }_1(i),6+{\delta }_2(i),6+{\delta }_3(i),1)-(6-{\delta }_1(i),6-{\delta }_2(i),6-{\delta }_3(i),1)]\\ & =(7,6,6,1)+(6,7,6,1)+(6,6,7,1)-(5,6,6,1)-(6,5,6,1)-(6,6,5,1)\\ {\pi }_2^{\prime }& =\sum _{i=1}^3[(6+{\delta }_1(i),6+{\delta }_2(i),6+{\delta }_3(i),1)-(6-{\delta }_1(i),6-{\delta }_2(i),6-{\delta }_3(i),11)]\\ & =(7,6,6,11)+(6,7,6,11)+(6,6,7,11)-(5,6,6,11)-(6,5,6,11)-(6,6,5,11).\end{array}$$

Remark: It would probably be simpler to just take ${\pi }_1$ as the input cycle.