2025-11-03

TL;DR: Co-dimension 2 OHCP in 4D still gives integral solutions.

---

The goal was to construct a 2-chain inside of the tetrahedralization of the unit 4D cube. We tackled the problem through marching tetrahedra.

We start by constructing a grid of points in $[-0.5,0.5{]}^4$. We did this by introducing a parameter $\gamma$ and constructing the following grid:

$$G=\{(-0.5+x/\gamma ,-0.5+y/\gamma ,-0.5+z/\gamma ,-0.5+w/\gamma ):x,y,z,w\in \{0,1,\dots ,\gamma \}\}.$$

This grid divides the unit 4D cube into smaller cubes, which we refer to as cells. Each cell is then tetrahedralized by Kuhn triangulation.

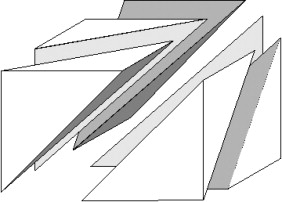
Kuhn triangulation divides an $n$-D cube into $n!$ tetrahedra (see 3D example above). Each tetrahedra is defined by a permutation of the $n$ spatial directions and origin point where all tetrahedra share the same origin point. The vertices of each tetrahedra correspond to a subset of the vertices of the cell.

With the Kuhn triangulation, each tetrahedra is cut to form the shape of our input surface. We define the input surface through an isosurface $f(x,y,z,w)=0$. More specifically, we took the 4D torus as the input:

$$f(x,y,z,w)={\left(\sqrt{x^2+y^2}-R\right)}^2+{\left(\sqrt{z^2+w^2}-R\right)}^2-r^2.$$

For each tetrahedra, we sample the isosurface at each of the four vertices ${\mathbf{v}}_0,\dots ,{\mathbf{v}}_3$. With the samples, we construct a binary code $b_3{b}_2{b}_1{b}_0$ indicating which vertices are inside/outside of the isosurface. More specifically,

$$b_i=\{\begin{array}{ll}1& f({\mathbf{v}}_i)>0\\ 0& f({\mathbf{v}}_i)\le 0.\end{array}$$

Using the binary code we construct (a) triangular face(s) of the surface based on the diagram below:

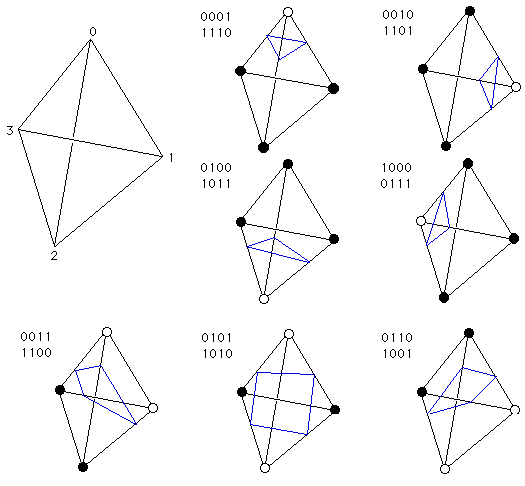
Since we need the isosurface to sit inside of a 4D cube, we pre-subdivide each tetrahedra so that each of the 8 possible cases above is the face of a smaller tetrahedra. Due to subdividing before sampling, we simply take the midpoint of two vertices instead of interpolating using the isovalue as is typical in marching tetrahedra. As a result, the isosurface appears blocky.

In our implementation, we use a resolution of $\gamma =10$. Resulting in $10^4$ cells, each of which are divided into 24 tetrahedra. Each tetrahedra has to be subdivided into 11 smaller tetrahedra to handle the 8 possible cases. As a result we ended up with 2,640,000 tetrahedra.

The code took a little over 3 hours to run. In the end, the relaxed OHCP LP still gave integral solutions. The example was also non-trivial as the 4D torus did not collapse into the empty chain.