4D Example Construction

Goal: Construct a 2-chain inside of the tetrahedralization of a unit 4D cube.

Method in 3D

We start with a simpler problem: constructing a 2-chain inside of the tetrahedralization of a unit 3D cube. The approach is based on marching tetrahedra, a variant of marching cubes.

The algorithm takes in two inputs:

1. An isosurface $f(\mathbf{x})=0$ that represents the target 2-chain
2. An integer $\gamma$ denoting the resolution for cube subdivision.

The first step is to take a unit cube centered at the origin and divide it into ${\gamma }^3$ smaller cubes, herein called cells. The set of cells form a tiling of the larger unit cube, with each cell being a $1/\gamma \times 1/\gamma \times 1/\gamma$ cube.

In the typical marching cubes algorithm, one would construct the 2-complex from these cells. However, we are interested in constructing a 3-complex containing the 2-complex. For that reason, we subdivide each cell into $3!=6$ tetrahedra via Kuhn triangulation. The Kuhn triangulation of a cube constructs a tetrahedra for each permutation of axis directions.

More precisely, consider a unit cube $C=[0,1{]}^n$. For each permutation $\pi \in S_n$, we construct the $n$-simplex given by the vertex set

$$\{0,e_{\pi (1)},e_{\pi (1)}+e_{\pi (2)},\dots ,e_{\pi (1)}+\cdots +e_{\pi (n)}\}$$

where $e_i$ is the $i$-th standard basis vector for ${\mathbb{R}}^n$. The corresponding simplices for $n=3$ are given below (image source):

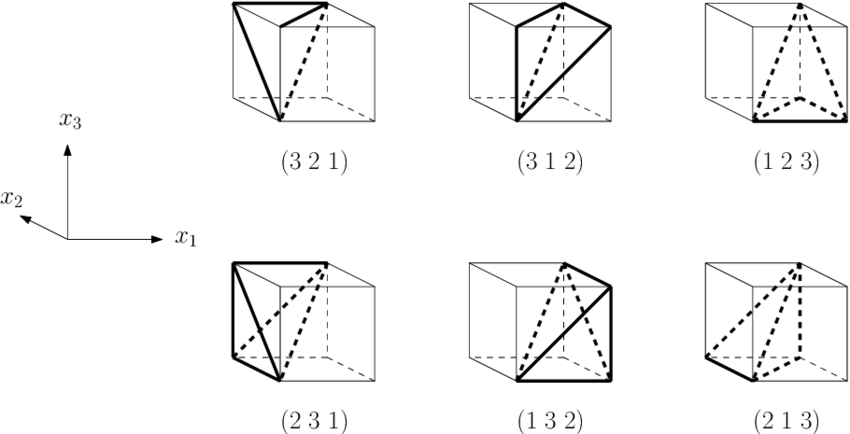
This procedure is done to each cell, resulting in a tetrahedralization of the original unit cube.

Claim: This is a valid 3-complex.

After constructing our 3-complex, we iterate over every tetrahedra with the goal of constructing our 2-complex homeomorphic to the isosurface $f(\mathbf{x})=0$. We take the simple 2-sphere given by

$$f(x,y,z)=x^2+y^2+z^2-{\left(\frac{1}{4}\right)}^2=0.$$

Given a tetrahedra with vertices ${\mathbf{v}}_0,\dots ,{\mathbf{v}}_3$, we sample the isofunction $f$ and construct a binary code $b_3{b}_2{b}_1{b}_0$ indicating which vertices are outside of the surface, i.e., we define

$$b_i=\{\begin{array}{ll}1& f({\mathbf{v}}_i)>0\\ 0& f({\mathbf{v}}_i)\le 0.\end{array}$$

The corresponding binary code is used to cut the tetrahedra and use the corresponding cut to form the 2-complex. The cuts are provided visually below (image source):

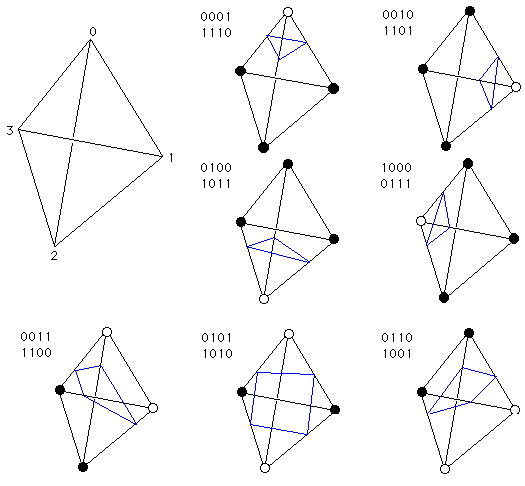Note that each binary code has a corresponding binary code (given by bit inversion) which has the faces oppositely oriented. The binary code $0000$ (and corresponding $1111$) indicate that the tetrahedra is entirely outside (inside) the isosurface and no cuts are necessary.

Typically, one forms the cuts by interpolating between the isovalues of adjacent vertices. However, for simplicity we simply take the midpoint and pre-cut the tetrahedra. As a consequence of this approach, we are required to perform every possible cut beforehand. The following figure designates the set of tetrahedra given after performing all possible cuts:

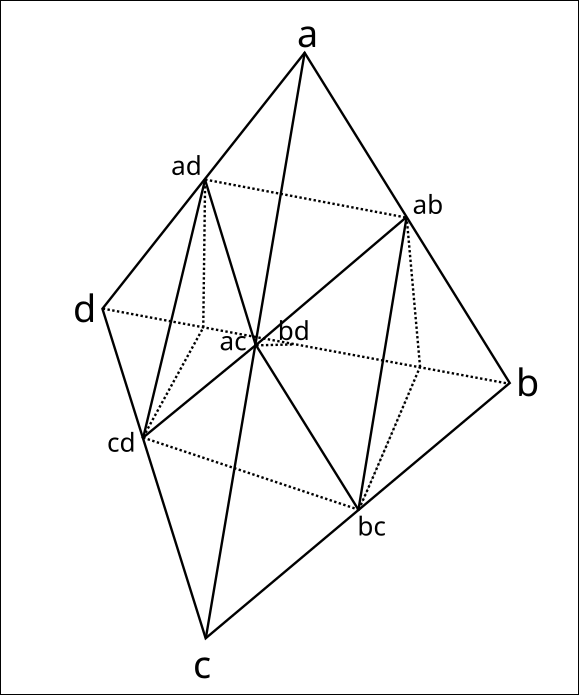
The full list of tetrahedra is as follows:

• 4 Corners:
  • $[a,ab,ac,ad]$
  • $[b,ab,bc,bd]$
  • $[c,ac,bc,cd]$
  • $[d,ad,bd,cd]$
• Inner Octahedron:
  • $[ad,ac,bd,cd]$
  • $[bd,bc,ac,cd]$
  • $[ab,cd,ad,ac]$
  • $[ab,bc,cd,ac]$
  • $[ab,bd,cd,bc]$
  • $[ab,ac,cd,bc]$
  • $[ab,ad,bd,center]$

The idea of pre-cutting the tetrahedra, is that we simply mark the corresponding triangles for the binary code to be part of the 2-chain.

Claim: For sufficiently high resolution $\gamma$, the resulting 2-chain is homeomorphic to the isosurface.

Extending to 4D

The majority of the above extends to 4D relatively easily. We need the following three modifications:

1. The initial unit cube is now a 4D cube that is split into ${\gamma }^4$ cells
2. We replace our 2-sphere input with a 3-sphere:

$$f(x,y,z,w)=x^2+y^2+z^2+w^2-{\left(\frac{1}{4}\right)}^2=0.$$

3. The Kuhn triangulation of a cell now gives a 4-complex. Since we are looking for a 3-complex, we simply take every face (checking for duplicates) of each corresponding 4-simplex.

Current Problem

I appear to be getting duplicate tetrahedra (exactly 3,000,000 duplicates). From my code, it appears to be occurring in the code where I cut up a tetrahedra as described above. Given that is done locally, and I do not see any duplicates in the list given, there must be two tetrahedra overlapping.