Isomorphism Theorems

First Isomorphism Theorem

Let $G$ and $H$ be groups and $f:G\to H$ a homomorphism. Then

1. $\text{Ker}f$ is a normal subgroup of $G$,
2. $\text{Im}f$ is a subgroup of $H$,
3. $\text{Im}f\cong G/\text{Ker}f$.

In particular, if $f$ is surjective then $H\cong G/\text{Ker}f$.

This is a consequence of the fundamental theorem on homomorphisms which is summarized by the following commutative diagram:

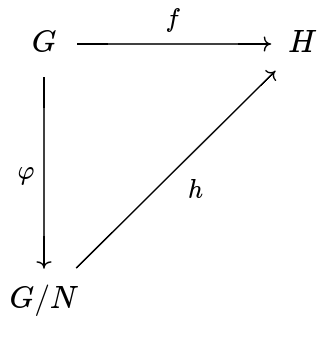
Fundamental Theorem on Homomorphisms

Let $G$ and $H$ be groups and $f:G\to H$ a homomorphism. Let $N$ be a normal subgroup of $G$ and $\phi :G\to G/N$ be given by $g\mapsto gN$. If $N$ is a subset of $\text{Ker}f$, then there is a unique homomorphism $g:G/N\to H$ such that $f=h\circ \phi$. Moreover, $h$ is injective if and only if $N=\text{Ker}f$.

The second isomorphism theorem can be summarized by the following diagram:

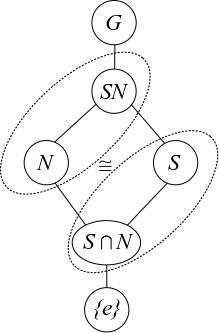
Second Isomorphism Theorem

Let $G$ be a group, $S<G$ and $N⊲G$. Then

1. The product $SN=\{sn:s\in S,n\in N\}$ is a subgroup of $G$,
2. $N$ is a normal subgroup of $SN$,
3. $S\cap N$ is a normal subgroup of $S$,
4. $(SN)/N$ and $S/(S\cap N)$ are isomorphic.

Some sources call this the diamond theorem or parallelogram theorem.