4. Differential Forms on Rn

The cotangent space at $p\in {\mathbb{R}}^n$, denoted $T_p^{\ast }({\mathbb{R}}^n)$, is the dual of the tangent space, i.e., $(T_p{\mathbb{R}}^n{)}^{\vee }$. Hence, a cotangent $f\in T_p^{\ast }({\mathbb{R}}^n)$ is a linear functional $f:T_p({\mathbb{R}}^n)\to \mathbb{R}$.

A covector field or a differential 1-form (1-form for short) on an open subset $U\subset {\mathbb{R}}^n$ is a map $\omega$ that assigns to each point $p\in U$ a covector

$$\begin{array}{r}\omega :U\to \bigcup _{p\in U}{T}_p^{\ast }({\mathbb{R}}^n)\\ p\mapsto {\omega }_p\in T_p^{\ast }({\mathbb{R}}^n).\end{array}$$

From any $C^{\infty }$ function $f:U\to \mathbb{R}$ we can construct a 1-form $df$ called the differential of $f$: for $p\in U$ and $X_p\in T_{p}U$ we define

$$(df{)}_p(X_p)=X_{p}f=\sum a^i(p)\frac{\partial f}{\partial x^i}{|}_p.$$

Example: Let $f:U\to \mathbb{R}$ represent temperature at at point $p\in U$. The differential of $f$, would take in a direction $X_p\in T_{p}U$ and give the change in temperature when traveling in the direction of $X_p$.

Recall that $\{\partial /\partial x^1{|}_p,\dots ,\partial /\partial x^n{|}_p\}$ is a basis for the tangent space $T_p({\mathbb{R}}^n)$.

Prp

If $x^1,\dots ,x^n$ are the standard coordinates on ${\mathbb{R}}^n$, then at each $p\in {\mathbb{R}}^n$, $\{(d{x}^1{)}_p,\dots ,(d{x}^n{)}_p\}$ is the basis for the cotangent space $T_p^{\ast }({\mathbb{R}}^n)$.

Proof: Notice that

$$(d{x}^i{)}_p\left(\frac{\partial }{\partial x^j}{|}_p\right)=\frac{\partial }{\partial x^j}{|}_p{x}^i={\delta }_j^i.$$

Q.E.D.

Thus, we can represent $\omega \in T_p^{\ast }({\mathbb{R}}^n)$ by the linear combination

$${\omega }_p=\sum a_i(p)(d{x}^i{)}_p$$

for some $a_i(p)\in \mathbb{R}$.

The differential $d{x}^i$ gives the $i$-th component of a vector field, i.e., if $X=\sum a^i\partial /\partial x^i$, then $(d{x}^i)(X)=a^i$.

Prp

If $f:U\to \mathbb{R}$ is a $C^{\infty }$ function on an open set $U$ in ${\mathbb{R}}^n$ then

$$df=\sum \frac{\partial f}{\partial x^i}d{x}^i.$$

Proof: From proposition 4.1, $df=\sum a_{i}d{x}^i$ for some functions $a_i:U\to \mathbb{R}$. Notice that

$$\frac{\partial f}{\partial x^j}=df\left(\frac{\partial }{\partial x^j}\right)=\sum a^{i}d{x}^i\left(\frac{\partial }{\partial x^j}\right)=\sum a_i{\delta }_j^i=a_j.$$

Q.E.D.

Differential k-Forms

A differential form of degree k or k-form $\omega$ on an open subset $U$ of ${\mathbb{R}}^n$ is a function that assigns to each point $p\in U$ an alternating $k$-linear function on the tangent space, i.e., $p\mapsto {\omega }_p\in A_k(T_p{\mathbb{R}}^n)$. Note that $A_1(T_p{\mathbb{R}}^n)=T_p^{\ast }({\mathbb{R}}^n$).

Recall that a basis for $A_k(T_p{\mathbb{R}}^n)$ is

$$d{x}_p^I=d{x}_p^{i_1}\wedge \cdots \wedge d{x}_p^{i_k},1\le i_1<\cdots <i_k\le n.$$

Therefore, at each point $p\in U$, ${\omega }_p$ is the linear combination

$${\omega }_p=\sum a_I(p)d{x}_p^I$$

so

$$\omega =\sum a_{I}d{x}^I$$

with function coefficients $a_I:U\to \mathbb{R}$. We say a $k$-form is $C^{\infty }$ on $U$ if each coefficient $a_I$ is $C^{\infty }$ on $U$. We denote the vector space of $C^{\infty }$ $k$-forms on $U$ by ${\Omega }^k(U)$.

Let $\omega$ be a $k$-form and $\tau$ an $\ell$-form on $U$. Then we define the wedge product of $\omega$ and $\tau$ to be the $(k+\ell )$-form defined pointwise:

$$(\omega \wedge \tau {)}_p={\omega }_p\wedge {\tau }_p.$$

In terms of coordinates, if $\omega =\sum a_{I}d{x}^I$ and $\tau =\sum b_{J}d{x}^J$, then

$$\omega \wedge \tau =\sum _{I,J}(a_I{b}_J)d{x}^I\wedge d{x}^J=\sum _{I,J\text{ disjoint}}(a_I{b}_J)d{x}^I\wedge d{x}^J.$$

One may show that the wedge product is anticommutative and associative.

Note that a 0-form maps a point $p\in U$ to an element of $A_0(T_p{\mathbb{R}}^n)$, an alternating 0-linear function, i.e., a constant function. Thus, a 0-form can be viewed simply as a function $\omega :U\to \mathbb{R}$. Notice then that if $f\in {\Omega }^0(U)$ and $\omega \in {\Omega }^k(U)$, then $f\wedge \omega$ is the $k$-form defined by pointwise multiplication

$$(f\wedge \omega {)}_p=f_p\wedge {\omega }_p=f(p){\omega }_p,$$

i.e., $f\wedge \omega =f\omega$.

Example: Let $x,y,z$ be the coordinates for ${\mathbb{R}}^3$. The $C^{\infty }$ 1-forms on ${\mathbb{R}}^3$ are of the form

$$fdx+gdy+hdz$$

where $f,g,h:{\mathbb{R}}^3\to \mathbb{R}$ are $C^{\infty }$ functions. The $C^{\infty }$ 2-forms are

$$fdy\wedge dz+gdx\wedge dz+hdx\wedge dy$$

and the $C^{\infty }$ 3-forms are

$$fdx\wedge dy\wedge dz.$$

There are no non-zero $k$-forms for $k>3$.

Differential Forms as Multilinear Functions on Vector Fields

Let $\omega$ be a $C^{\infty }$ 1-form and $X$ a $C^{\infty }$ vector field on $U\subset {\mathbb{R}}^n$. We define $\omega (X)$ on $U$ by

$$\omega (X{)}_p={\omega }_p(X_p)$$

or if $\omega =\sum a_{i}d{x}^i$ and $X=\sum b^j\frac{\partial }{\partial x^j}$, then

$$w(X)=\left(\sum a_{i}d{x}^i\right)\left(\sum b^j\frac{\partial }{\partial x^j}\right)=\sum a_i{b}^i.$$

Thus, a $C^{\infty }$ 1-form gives rise to map between vector fields $\mathfrak{X}(U)$ to smooth functions $C^{\infty }(U)$. This function is linear over the ring $C^{\infty }(U)$, i.e., if $f\in C^{\infty }(U)$ then

$$\omega (fX)=f\omega (X).$$

Indeed, let $p\in U$ and notice that

$$\begin{array}{rl}(\omega (fX){)}_p& ={\omega }_p(f(p)X_p)=f(p){\omega }_p(X_p)=(f\omega (X){)}_p.\end{array}$$

Thus a 1-form $\omega$ on $U$ gives rise to an $C^{\infty }(U)$-linear map $\mathfrak{X}(U)\to C^{\infty }(U)$ given by $X\mapsto \omega (X)$. Likewise, a $k$-form $\omega$ gives rise to a $k$-linear map

$$\begin{array}{r}\mathfrak{X}(U)\times \cdots \times \mathfrak{X}(U)\to C^{\infty }(U)\\ (X_1,\dots ,X_k)\mapsto \omega (X_1,\dots ,X_k).\end{array}$$

The Exterior Derivative

Let $f:U\to \mathbb{R}$ be $C^{\infty }$. We define the exterior derivative of $f$ to be the differential $df\in {\Omega }^1(U)$ given by

$$df=\sum \frac{\partial f}{\partial x^i}d{x}^i.$$

We then can use this definition to define the exterior derivative of a $k$-form.

Def

For $k\ge 1$, if $\omega ={\sum }_I{a}_{I}d{x}^I\in {\Omega }^k(U)$, then the exterior derivative is given by

$$d\omega =\sum _{I}d{a}_I\wedge d{x}^I=\sum _I\left(\sum _j\frac{\partial a_I}{\partial x^j}d{x}^j\right)\wedge d{x}^I\in {\Omega }^{k+1}(U).$$

Example: Consider the 1-form $fdx+gdy$ on ${\mathbb{R}}^2$, where $f,g:{\mathbb{R}}^2\to \mathbb{R}$ are $C^{\infty }$. Then

$$\begin{array}{rl}d\omega & =df\wedge dx+dg\wedge dy\\ & =\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)\wedge dx+\left(\frac{\partial g}{\partial x}dx+\frac{\partial g}{\partial y}dy\right)\wedge dy\\ & =\frac{\partial f}{\partial x}dx\wedge dx+\frac{\partial f}{\partial y}dy\wedge dx+\frac{\partial g}{\partial x}dx\wedge dy+\frac{\partial g}{\partial y}dy\wedge dy\\ & =\left(\frac{\partial g}{\partial x}-\frac{\partial f}{\partial y}\right)dx\wedge dy.\end{array}$$

Def

Let $A={⨁}_{k=0}^{\infty }{A}^k$ be a graded algebra over a field $K$. An antiderivation of a graded algebra $A$ is a $K$-linear map $D:A\to A$ such that for $a\in A^k$ and $b\in A^{\ell }$,

$$D(ab)=(Da)b+(-1{)}^{k}aDb.$$

If $D$ sends $A^k$ to $A^{k+m}$ for all $k$, then we say that has degree $m$.

Prp

1. The exterior differentiation $d:{\Omega }^{\ast }(U)\to {\Omega }^{\ast }(U)$ is an antiderivation of degree 1:

$$d(\omega \wedge \tau )=(d\omega )\wedge \tau +(-1{)}^{\text{deg}\omega }\omega \wedge d\tau$$

2. $d^2=0$
3. If $f\in C^{\infty }(U)$ and $X\in \mathfrak{X}(U)$, then $(df)(X)=Xf$.

Proof:

1. Let $\omega =fd{x}^I$ and $\tau =gd{x}^J$. Notice that

$$\begin{array}{rl}d(\omega \wedge \tau )& =d(fgd{x}^I\wedge d{x}^J)\\ & =\sum \frac{\partial fg}{\partial x^i}d{x}^i\wedge d{x}^I\wedge d{x}^J\\ & =\sum \frac{\partial f}{\partial x^i}gd{x}^i\wedge d{x}^I\wedge d{x}^J+\sum f\frac{\partial g}{\partial x^i}d{x}^i\wedge d{x}^I\wedge d{x}^J\\ & =\sum \frac{\partial f}{\partial x^i}d{x}^i\wedge d{x}^I\wedge gd{x}^J+(-1{)}^k\sum fd{x}^I\wedge \frac{\partial g}{\partial x^i}d{x}^i\wedge d{x}^J\\ & =d\omega \wedge \tau +(-1{)}^k\omega \wedge d\tau .\end{array}$$

The rest follows by linearity.

2. Let $\omega =fd{x}^I$. Notice that

$$\begin{array}{rl}{d}^2\omega & =d\left(\sum \frac{\partial f}{\partial x^i}d{x}^i\wedge d{x}^I\right)=\sum \frac{{\partial }^{2}f}{\partial x^j\partial x^i}d{x}^j\wedge d{x}^i\wedge d{x}^I.\end{array}$$

In the sum, when $i=j$ we get $d{x}^j\wedge d{x}^i=0$. For $i\ne j$, the two symmetric terms cancel

$$\frac{{\partial }^2}{\partial x^i\partial x^j}d{x}^i\wedge d{x}^j+\frac{{\partial }^2}{\partial x^j\partial x^i}d{x}^j\wedge d{x}^i=\frac{{\partial }^{2}f}{\partial x^i\partial x^j}d{x}^i\wedge d{x}^j+\frac{{\partial }^{2}f}{\partial x^i\partial x^j}(-d{x}^i\wedge d{x}^j)=0.$$

Therefore, $d^2\omega =0$.

3. Notice that for $X=\sum b^j\frac{\partial }{\partial x^j}$,

$$(df)(X)=\left(\sum \frac{\partial f}{\partial x^i}d{x}^i\right)(X)=\sum \frac{\partial f}{\partial x^i}{b}^i=Xf.$$

Q.E.D.

> [!prp] > > If $D:\Omega^*(U)\rightarrow\Omega^*(U)$ satisfies properties (1)-(3) in the previous proposition, then $D=d$.

Closed Forms and Exact Forms

A $k$-form on $U$ is closed if $d\omega =0$; it is exact if there is a $(k-1)$-form $\tau$ such that $\omega =d\tau$ on $U$. Since $d^2=0$, every exact form is closed.

Example: Define the 1-form $\omega$ on ${\mathbb{R}}^2\setminus \{0\}$ by

$$\omega =\frac{1}{x^2+y^2}(-ydx+xdy).$$

Notice that

$$\begin{array}{rl}d\omega & =\left(\frac{2xy}{(x^2+y^2{)}^2}dx+\frac{y^2-x^2}{(x^2+y^2{)}^2}dy\right)\wedge dx+\left(\frac{y^2-x^2}{(x^2+y^2{)}^2}dx-\frac{2xy}{(x^2+y^2{)}^2}dy\right)\wedge dy\\ & =\frac{y^2-x^2}{(x^2+y^2{)}^2}dy\wedge dx+\frac{y^2-x^2}{(x^2+y^2{)}^2}dx\wedge dy\\ & =-\frac{y^2-x^2}{(x^2+y^2{)}^2}dx\wedge dy+\frac{y^2-x^2}{(x^2+y^2{)}^2}dx\wedge dy\\ & =0.\end{array}$$

Therefore, $\omega$ is closed.

For any open subset $U\subset {\mathbb{R}}^n$, the exterior derivative $d$ forms a differential complex called the de Rham complex of $U$ given by

$$0\stackrel{d}{\to }{\Omega }^0(U)\stackrel{d}{\to }{\Omega }^1(U)\stackrel{d}{\to }{\Omega }^2(U)\stackrel{d}{\to }\cdots .$$

The closed forms are in the kernel of $d$, and the exact forms are in the image of $d$.

From here, we can define the $k$-th de Rham cohomology of $U$ to be the quotient vector space

$$H^k(U):=\frac{\text{Ker}d}{\text{Im}d}.$$

Poincare

For $k\ge 1$, every closed $k$-form on ${\mathbb{R}}^n$ is exact.

This is equivalent to saying that the de Rham cohomology $H^k({\mathbb{R}}^n)$ is trivial for $k\ge 1$.

Applications to Vector Calculus

A vector-valued function is a function $\text{F}:⟨P,Q,R⟩:U\to {\mathbb{R}}^3$ that assigns to each point $p\in U$ a vector $F_p\in {\mathbb{R}}^3\cong T_p({\mathbb{R}}^3)$. Hence, a vector-valued function on $U$ is a vector field on $U$. Recall that

$$\begin{array}{rl}\text{grad}f& =\nabla \cdot f=⟨\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}⟩,\\ \text{curl}\text{F}& =\nabla \times \text{F}=⟨\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z},\frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x},\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}⟩\\ \text{div}\text{F}& =\nabla \cdot \text{F}=\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z}.\end{array}$$

Since a 1-form on $U$ is a linear combination of $dx$, $dy$, $dz$, we can identify 1-forms via vectors

$$Pdx+Qdy+Rdz⟷⟨P,Q,R⟩$$

and 2-forms

$$Pdy\wedge dz+Qdz\wedge dx+Rdx\wedge dy⟷⟨P,Q,R⟩$$

and 3-forms

$$fdx\wedge dy\wedge dz⟷f.$$

In this form, we can see that

$$\begin{array}{rl}df& ⟷\text{grad}f\\ d(Pdx+Qdy+Rdz)& ⟷\text{curl}⟨P,Q,R⟩\\ d(Pdy\wedge dz+Qdz\wedge dx+Rdx\wedge dy)& ⟷\text{div}⟨P,Q,R⟩.\end{array}$$

In other words, the gradient is the exterior derivative on a 0-form. The curl is the exterior derivative on a 1-form, and the divergence is the exterior derivative on a 2-form. Or, in visual terms:

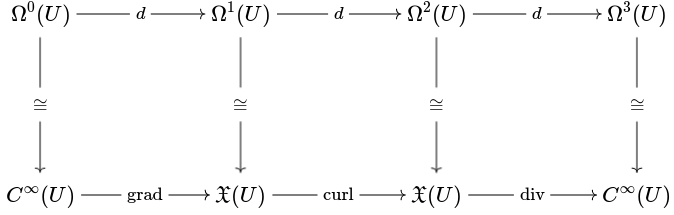
From this identification, we easy get the following proposition.

Prp

1. $\text{curl}(\text{grad}f)=0$
2. $\text{div}(\text{curl}f)=0$
3. On ${\mathbb{R}}^3$, a vector field $\text{F}$ is the gradient of some scalar $f$ if and only if $\text{curl}\text{F}=0$.

Proof: Properties 1 and 2 follow from the property $d^2=0$. Property 3 is due to the Poincare lemma.

Q.E.D.

Note that property 3 may not hold on a region other than $\R^3$.

Example: If $U={\mathbb{R}}^3\setminus \{z\text{-axis}\}$ and

$$\text{F}=⟨\frac{-y}{x^2+y^2},\frac{x}{x^2+y^2},0⟩$$

on ${\mathbb{R}}^3$, then $\text{curl}\text{F}=0$, but $\text{F}$ is not the gradient of any $C^{\infty }$ function on $U$. Assume it was. Then by the fundamental theorem of calculus for line integrals

$${\int }_C-\frac{y}{x^2+y^2}dx+\frac{x}{x^2+y^2}dy=0$$

for any closed curve $C$. However, on the unit circle with $x=\cos t$ and $y=\sin t$ we get

$${\int }_C-\frac{y}{x^2+y^2}dx+\frac{x}{x^2+y^2}dy={\int }_0^{2\pi }-(\sin t)d\cos t+(\cos t)d\sin t={\int }_0^{2\pi }dt=2\pi .$$

A contradiction.

Problems

4.1. A 1-form on ${\mathbb{R}}^3$

Let $\omega$ be the 1-form $zdx-dz$ and $X$ be the vector filed $y\partial /\partial x+x\partial /\partial y$ on ${\mathbb{R}}^3$. Compute $\omega (X)$ and $d\omega$.

Answer: Notice that

$$\begin{array}{rl}\omega (X)& =(zdx-dz)\left(y\frac{\partial }{\partial x}+x\frac{\partial }{\partial y}\right)=zy\end{array}$$

Notice that for a 1-form $\omega =f_{1}d{x}^1+f_{2}d{x}^2+f_{3}d{x}^3$ in ${\mathbb{R}}^3$,

$$\begin{array}{rl}d\omega & =\sum _{i=1}^3\left(\sum _{j=1}^3\frac{\partial f_i}{\partial x^j}d{x}^j\right)\wedge d{x}^i\\ & =\left(\sum _{j=1}^3\frac{\partial f_1}{\partial x^j}d{x}^j\right)\wedge d{x}^1+\left(\sum _{j=1}^3\frac{\partial f_2}{\partial x^j}d{x}^j\right)\wedge d{x}^2+\left(\sum _{j=1}^3\frac{\partial f_3}{\partial x^j}d{x}^j\right)\wedge d{x}^3\\ & =\frac{\partial f_1}{\partial x^2}d{x}^2\wedge d{x}^1+\frac{\partial f_1}{\partial x^3}d{x}^3\wedge d{x}^1\\ & +\frac{\partial f_2}{\partial x^1}d{x}^1\wedge d{x}^2+\frac{\partial f_2}{\partial x^3}d{x}^3\wedge d{x}^2\\ & +\frac{\partial f_3}{\partial x^1}d{x}^1\wedge d{x}^3+\frac{\partial f_3}{\partial x^2}d{x}^2\wedge d{x}^3\\ & =\left(\frac{\partial f_2}{\partial x^1}-\frac{\partial f_1}{\partial x_2}\right)d{x}^1\wedge d{x}^2+\left(\frac{\partial f_3}{\partial x^1}-\frac{\partial f_1}{\partial x_3}\right)d{x}^1\wedge d{x}^3+\left(\frac{\partial f_3}{\partial x^2}-\frac{\partial f_2}{\partial x_3}\right)d{x}^2\wedge d{x}^3\end{array}$$

Therefore,

$$d(zdx-dz)=-dx\wedge dz$$

4.2. A 2-form on ${\mathbb{R}}^3$

At each point $p\in {\mathbb{R}}^3$, define a bilinear function ${\omega }_p$ on $T_p({\mathbb{R}}^3)$ by

$${\omega }_p(a,b)=p^3\det \left[\begin{array}{cc}{a}^1& b^1\\ a^2& b^2\end{array}\right],$$

for tangent vectors $a,b\in T_p({\mathbb{R}}^3)$, where $p^3$ is the third component of $p=(p^1,p^2,p^3)$. Since ${\omega }_p$ is an alternating bilinear function on $T_p({\mathbb{R}}^3)$, $\omega$ is a 2-form on ${\mathbb{R}}^3$. Write $\omega$ in terms of the standard basis $d{x}^i\wedge d{x}^j$ at each point.

Answer: We want functions $f,g,h:{\mathbb{R}}^3\to \mathbb{R}$ such that

$$\omega =fd{x}^1\wedge d{x}^2+gd{x}^1\wedge d{x}^3+hd{x}^2\wedge d{x}^3.$$

Recall that if ${\alpha }^1,{\alpha }^2$ are linear functions and $v_1,v_2$ are vectors then

$$({\alpha }^1\wedge {\alpha }^2)(v_1,v_2)=\det \left[\begin{array}{cc}{\alpha }^1(v_1)& {\alpha }^1(v_2)\\ {\alpha }^2(v_1)& {\alpha }^2(v_2)\end{array}\right].$$

So

$$(x^i\wedge x^j)(a,b)=\det \left[\begin{array}{cc}{a}^i& b^i\\ a^j& b^j\end{array}\right].$$

Therefore, letting $f(p)=p^3$ and $g=h=0$ gives us

$${\omega }_p(a,b)=f(p)(d{x}^1\wedge d{x}^2)(a,b)=p^3\det \left[\begin{array}{cc}{a}^1& b^1\\ a^2& b^2\end{array}\right].$$

4.3. Exterior calculus

Suppose the standard coordinates on ${\mathbb{R}}^2$ are called $r$ and $\theta$ (this ${\mathbb{R}}^2$ is the $(r,\theta )$-plane, not the $(x,y)$-plane). If $x=r\cos \theta$ and $y=r\sin \theta$, calculate $dx$, $dy$ and $dx\wedge dy$ in terms of $dr$ and $d\theta$.

Answer: Notice that

$$dx=\frac{\partial x}{\partial r}dr+\frac{\partial x}{\partial \theta }d\theta =\cos \theta dr-r\sin \theta d\theta$$

and

$$dy=\frac{\partial y}{\partial r}dr+\frac{\partial y}{\partial \theta }d\theta =\sin \theta dr+r\cos \theta d\theta .$$

Therefore,

$$\begin{array}{rl}dx\wedge dy& =(\cos \theta dr-r\sin \theta d\theta )\wedge (\sin \theta dr+r\cos \theta d\theta )\\ & =r{\cos }^2\theta dr\wedge d\theta -r{\sin }^{2}d\theta \wedge dr\\ & =(r{\cos }^2\theta +r{\sin }^2\theta )dr\wedge d\theta \\ & =rdr\wedge d\theta .\end{array}$$

4.4. Exterior calculus

Suppose the standard coordinates on ${\mathbb{R}}^3$ are called $\rho$, $\varphi$ and $\theta$. If $x=\rho \sin \varphi \cos \theta$, $y=\rho \sin \varphi \sin \theta$ and $z=\rho \cos \varphi$, calculate $dx$, $dy$, $dz$ and $dx\wedge dy\wedge dz$ in terms of $d\rho$, $d\varphi$ and $d\theta$.

Answer: Notice that

$$\begin{array}{rl}dx& =\frac{\partial x}{\partial \rho }d\rho +\frac{\partial x}{\partial \varphi }d\varphi +\frac{\partial x}{\partial \theta }d\theta =\sin \varphi \cos \theta d\rho +\rho \cos \varphi \cos \theta d\varphi -\rho \sin \varphi \sin \theta d\theta \\ dy& =\frac{\partial y}{\partial \rho }d\rho +\frac{\partial y}{\partial \varphi }d\varphi +\frac{\partial y}{\partial \theta }d\theta =\sin \varphi \sin \theta d\rho +\rho \cos \varphi \sin \theta d\varphi +\rho \sin \varphi \cos \theta d\theta \\ dz& =\frac{\partial z}{\partial \rho }d\rho +\frac{\partial z}{\partial \varphi }d\varphi +\frac{\partial z}{\partial \theta }d\theta =\cos \varphi d\rho -\rho \sin \varphi d\varphi \end{array}$$

Therefore,

$$\begin{array}{rl}dx\wedge dy\wedge dz& =(dx\wedge dy)\wedge dz\\ & =[(\rho \sin \varphi \cos \theta \cos \varphi \sin \theta -\rho \cos \varphi \cos \theta \sin \varphi \sin \theta )d\rho \wedge d\varphi \\ & +(\rho {\sin }^2\varphi {\cos }^2\theta +\rho {\sin }^2\varphi {\sin }^2\theta )d\rho \wedge d\theta \\ & +({\rho }^2\cos \varphi \sin \varphi {\cos }^2\theta +{\rho }^2\sin \varphi \cos \varphi {\sin }^2\theta )d\varphi \wedge d\theta \\ & ]\wedge dz\\ & =\left(\rho {\sin }^2\varphi d\rho \wedge d\theta +{\rho }^2\sin \varphi \cos \varphi d\varphi \wedge d\theta \right)\wedge dz\\ & =(-{\rho }^2{\sin }^3\varphi )d\rho \wedge d\theta \wedge d\varphi +({\rho }^2\sin \varphi {\cos }^2\varphi )d\varphi \wedge d\theta \wedge d\rho \\ & =({\rho }^2\sin \varphi )d\varphi \wedge d\theta \wedge d\rho \end{array}$$