The Directional Derivative
One may visualize the tangent space at as the vector space of arrows emanating from tangentially. We write vectors by . We denote the standard basis for by . Hence, . We call vectors tangent vectors.
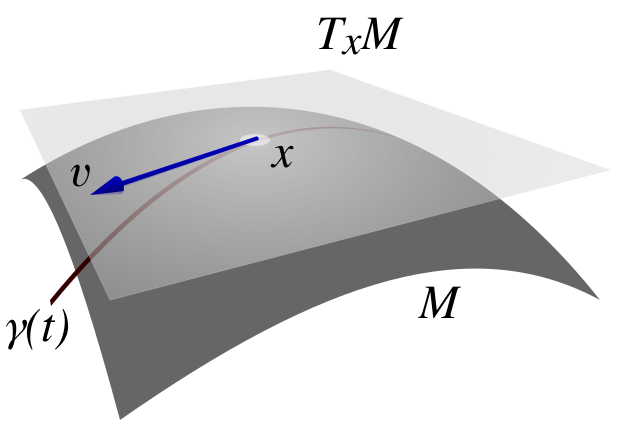
If is in a neighborhood of and , we define the directional derivative of in the direction of at by
Notice that
Note that is a number, not a function. We write
for the map that sends a function to .
Germs of Functions
Equivalence Relation
A relation on a set is a subset . We say for if . The relation is an equivalence relation if for all
- if , then
- If and , then .
Let where is a neighborhood of and is . We say that is equivalent to if there is an open set containing such that when restricted to . The equivalence class of is called the germ of at . We write for the set of all germs of functions on at .
Example: The functions
with domain and
with domain have the same germ at any point because is the geometric series
which converges to for all .
Algebra
An algebra over a field is a vector space over with a multiplication map such that for all and
- and
- .
Note that an algebra has three operations, addition, multiplication from the ring, and multiplication from the vector space.
Linear map
A map between vector spaces over a field is called a linear map if for any and ,
If and are algebras over a field , then an algebra homomorphism is a linear map such that for all .
Prp
is an algebra over .
Proof: Let and . Define to be the germ and to be the germ . Notice that
and
Next, notice that
and
Finally, we define to be the germ . Then one may see that
Therefore, is an algebra over .
Q.E.D.
Derivations at a Point
Notice that for each tangent vector , the directional derivative at gives a map of real vector spaces
which maps germs to their directional derivative at . One may show that is -linear and satisfies the Leibniz rule
Indeed, notice that
and
As for Leibniz’s rule,
In general, any linear map satisfying Leibniz rule is called a derivation at . We denote the set of all derivations at by . It follows that all directional derivatives at a point are derivations at by the map
Lemma
If is a point-derivation of , then for any constant function .
Proof: Notice that by -linearity, . So it suffices to show that . By making use of Leibniz’s rule,
which holds if and only if .
Q.E.D.
Thm
The linear map defined in (1) is an isomorphism of vector spaces.
Proof: We need to show that is a bijection and is linear. Suppose . Then it follows that
where is the Kronecker delta. This holds for all , hence .
Now let be a point-derivation at . Consider a germ in such that is star-shaped. By Taylor’s thoerem,
Notice that by applying to both sides
Thus, where for all . Hence is surjective.
Linearity is trivial.
Q.E.D.
As a result, the standard basis for corresponds to the partial derivatives .
Vector Fields
Def
A vector field on a subset of is a function that assigns to each point a tangent vector .
The vector can be expressed as a linear combination
Thus, one may view the vector space as the linear combination
where are some functions. We say is if each coefficient function is . One may identify vector fields on with column vectors:
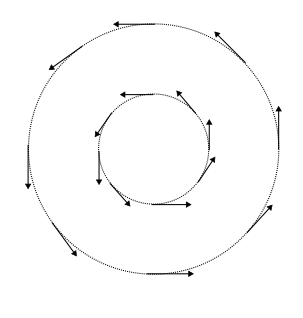
Example: On let . Then
is the vector field below:
One may define multiplication of vector fields by functions on pointwise:
Notice that if is a vector field, and is a function on , then is a vector field on . Hence, the set of all vector fields on , denoted , is a module over the ring ).
Def
If is a commutative ring with identity, then a (left) -module is an abelian group with a scalar multiplication map such that for all and
- , .
Def
Let and be -modules. An -module homomorphism from to is a map such that
- .
Vector Fields as Derivations
Let be a vector field on and a function. Then we define a new function by
Thus, a vector field gives rise to an -linear map
We claim this map is a derivation.
Prp
If is a vector field and and are functions on , then satisfies Leibniz rule
Proof: Notice that for
This holds for every point .
Q.E.D.
Problems
2.1. Vector fields
Let be the vector field and on . Compute .
Answer:
2.3. Vector space structure on derivations at a point
Let and be derivations at in , and . Prove that the sum and the scalar multiple are derivations at .
Answer: Clearly they are linear, so we simply need to show they satisfy Leibniz’s rule. Notice that
Furthermore,