Functoriality

Since categories are mathematical objects, it leads to the question of morphisms between categories.

Functor

A functor $F:C\to D$ between categories satisfies

• An object $Fc\in D$ for each $c\in C$
• A morphism $Ff:Fc\to F{c}^{\prime }\in D$ for each morphism $f:c\to c^{\prime }\in C$

The following functoriality axioms must hold:

• For any composable $f,g$ in $C$, $Fg\cdot Ff=F(g\cdot f)$
• For each $c\in C$, $F(1_c)=1_{Fc}$

A functor is a mapping of objects and morphisms that preserves the structure of a category.

Some examples:

• The endofunctor $P:\text{Set}\to \text{Set}$ given by taking a set $A$ to its power set $\mathcal{P}(A)$ and function $f:A\to B$ to the direct-image function $f_{\ast }:\mathcal{P}(A)\to \mathcal{P}(B)$ which maps $A^{\prime }\subset A$ to the image $f(A^{\prime })\subset B$.

• Concrete categories have the forgetful functor which sends objects to their underlying sets and morphisms to their underlying function.

• The fundamental group is a functor ${\pi }_1:{\text{Top}}_{\ast }\to \text{Group}$ that maps continuous functions $f:(X,x)\to (Y,y)$ to group homomorphisms $f_{\ast }:{\pi }_1(X,x)\to {\pi }_1(Y,y)$.

We can use functors to prove various results about spaces. For example, consider Brouwer’s fixed point theorem which states any continuous endomorphism of a 2-dimensional disk $D^2$ has a fixed point:

For the sake of contradiction let $f:D^2\to D^2$ such that $f(x)\ne x$ for all $x\in D^2$. Consider the continuous function $r:D^2\to S^1$ which casts a ray from the disks center through $x$ onto the boundary $S^1$. As a result $r$ defines a retraction on the inclusion $i:S^1\hookrightarrow D^2$, i.e., $ir=1_{S^1}$.

For any any basepoint on $S^1$ apply the functor ${\pi }_1$ to get a pair of group homomorphisms

$${\pi }_1(S^1)\stackrel{{\pi }_1(i)}{\to }{\pi }_1(D^2)\stackrel{{\pi }_1(r)}{\to }{\pi }_1(S^1).$$

By the functoriality axioms

$${\pi }_1(r)\cdot {\pi }_1(i)={\pi }_1(ri)={\pi }_1(1_{S^1})=1_{{\pi }_1(S^1)}.$$

But ${\pi }_1(S^1)=\mathbb{Z}$ and ${\pi }_1(D^2)=0$. So we expect ${\pi }_1(r)\cdot {\pi }_1(i)$ to be the zero endomorphism. A contradiction.

Contravariant functor

A contravariant functor $F$ from $C$ to $D$ is a functor $F:C^{\text{op}}\to D$ satisfies

• An object $Fc\in D$ for each $c\in C$
• A morphism $Ff:F{c}^{\prime }\to Fc\in D$ for each morphism $f:c\to c^{\prime }\in C$

The following functoriality axioms must hold:

• For any composable $f,g$ in $C$ $Ff\cdot Fg=F(g\cdot f)$
• For each $c\in C$, $F(1_c)=1_{Fc}$

The difference between (covariant) functors and contravariant functors can be summed up with the following diagram:

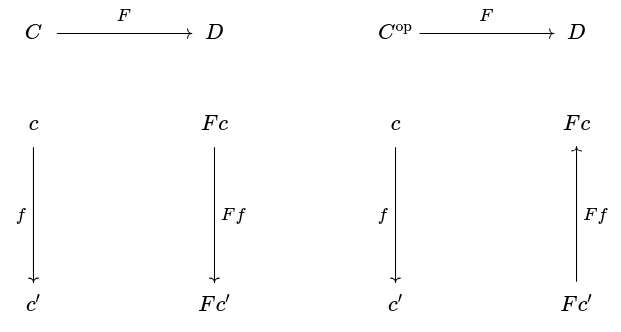
Some examples:

• The contravariant power set functor $P:{\text{Set}}^{\text{op}}\to \text{Set}$ sends a set $A$ to its power set $\mathcal{P}(A)$ and a function $f:A\to B$ to the inverse-image function $f^{-1}:\mathcal{P}(B)\to \mathcal{P}(A)$ that maps $B^{\prime }\subset B$ to $f^{-1}(B)\subset A$.
• The functor $\mathcal{O}:{\text{Top}}^{\text{op}}\to \text{Poset}$ carries spaces $X$ to its poset $\mathcal{O}(X)$ of open subsets.

Lemma

Functors preserve isomorphism.

Proof: Let $F:C\to D$ be a functor and $f:x\to y$ an isomorphism in $C$ with inverse $g:y\to x$. By the functoriality axioms,

$$F(g)F(f)=F(gf)=F(1_x)=1_{Fx}$$

and

$$F(f)F(g)=F(fg)=F(1_y)=1_{Fy}.$$

Note that a functor may not preserve monomorphisms or epimorphisms. But it does preserve split monomorphisms and split epimorphisms.

Def

If $C$ is locally small, then for any $c\in C$ we get a pair of covariant and contravariant functors represented by $c$:

• the functor $C(c,-):C\to \text{Set}$ carries $x\in C$ to $C(c,x)$ and morphisms $f:x\to y$ to post-composition $f_{\ast }:C(c,x)\to C(c,y)$
• the functor $C(-,c):C^{\text{op}}\to \text{Set}$ carries $c\in C$ to $C(x,c)$ and morphisms $f:x\to y$ to pre-composition $f^{\ast }:C(y,c)\to C(x,c)$.

The pair of functors in the previous definition can be encoded into a single bifunctor, i.e., a functor with two variables.

Product

For categories $C,D$ their product is the category $C\times D$ where

• objects are ordered pairs $(c,d)$
• morphisms are ordered pairs $(f,g):(c,d)\to (c^{\prime },d^{\prime })$
• composition and identities are defined componentwise.

Two-sided represented functor

If $C$ is locally small, then there is a two-sided represented functor $C(-,-):C^{\text{op}}\times C\to \text{Set}$ where a pair of objects $(x,y)$ are mapped to the hom-set $C(x,y)$ and a pair of morphisms $f:w\to x$ and $h:y\to z$ is sent to the function which maps $g:x\to y\in C(x,y)$ to $hgf:w\to z\in C(w,z)$.