2024-10-07

We seek a counter example that shows that the Steinhaus filtration is not always $q$-tame.

Construct the following data set

$$X=\{0,1\}\times \mathbb{N}.$$

Our lens $f:X\to \mathbb{R}$ we define by $(n,x)\mapsto n$, i.e., project onto $\mathbb{N}$. Cover the projection with the cover elements

$$\{\left(n-1,n+1\right)\mid n\in \mathbb{N}\}.$$

Thus under the MAPPER our cover is then

$$\mathcal{U}=\{B_1(x,n)\mid (x,n)\in X\}.$$

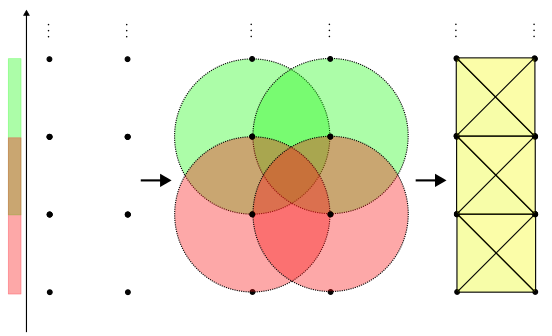
Consider two adjacent balls $U_1$ and $U_2$, then

$$d_{St}(U_1,U_2)=1-\frac{\mu (U_1\cap U_2)}{\mu (U_1\cup U_2)}.$$

According to https://math.stackexchange.com/questions/402858/area-of-intersection-between-two-circles the area of the intersection is

$$\mu (U_1\cap U_2)=1^2\left(\frac{2\pi }{3}-\frac{\sqrt{3}}{2}\right)=\frac{6\pi -3\sqrt{3}}{6}.$$

So the Steinhaus distance between two balls is

$$1-\frac{6\pi -3\sqrt{3}}{6\pi +3\sqrt{3}}\approx \mathrm{0.432.}$$

We now consider three adjacent balls $U_1,U_2$ and $U_3$. According to https://www.benfrederickson.com/calculating-the-intersection-of-3-or-more-circles/,

$$\mu (U_1\cap U_2\cap U_3)\approx \mathrm{0.44297.}$$

So

$$\mu (U_1\cup U_2\cup U_3)=3\pi 1^2-\mu (U_1\cap U_2)-\mu (U_2\cap U_3)=\frac{3\pi +3\sqrt{3}}{3}.$$

Thus, the Steinhaus distance between three balls is approximately

$$1-\frac{3\cdot 0.432}{3\pi +3\sqrt{3}}\approx \mathrm{0.911.}$$

In other words, in our Steinhaus filtration triangles are not born until about $\alpha \approx 0.911$.

Notice that for all $t\in \mathbb{N}$, the edge $e_t=[(0,t),(1,t)]$ is in ${\text{Nrv}}_{St}(\mathcal{U},0.432)$ but it is not on the boundary of a triangle. Define the cycle

$${\gamma }_t=[(0,t),(0,t+1)]+[(0,t+1),(1,t+1)]-[(1,t),(1,t+1)]-[(0,t),(1,t)].$$

The cycles $\{{\gamma }_t{\}}_{t\in \mathbb{N}}$ forms a linearly independent set; thus, the first homology group has infinite dimension. But for $\alpha <0.432$, the first homology group of ${\text{Nrv}}_{St}(\mathcal{U},\alpha )$ is trivial. Therefore, there is at least one map in the persistence module that has infinite rank, i.e., it is not $q$-tame.