Network Search Algorithms

Given a network $G=(N,A)$, we wish to find paths from a source node $s$ to every reachable node $i\in N$. There are several algorithms which can do this for us with various pros and cons, we focus on generic search.

In generic search, nodes are in one of two states: marked or unmarked. All marked nodes are known to be reachable from our source node $s$. Notice that if $i$ is marked, $j$ is unmarked and the network has an arc $(i,j)$, then we can mark node $j$. We refer to arcs $(i,j)$ as admissible if node $i$ is marked and node $j$ is unmarked. Otherwise, the arc is inadmissible.

The search algorithm will traverse the marked nodes in a certain order. We track this order with an array $\text{order}$ where $\text{order}(i)$ is the order of node $i$ in the traversal. We also keep track of a second array $\text{pred}$ where $\text{pred}(j)=i$ indicates that we marked node $j$ after traveling along arc $(i,j)$. The combination of $\text{order}$ and $\text{pred}$ define a search tree on the nodes in $G$ which contains all nodes reachable from $s$.

The algorithm also keeps track of a list of nodes $\text{LIST}$ which contains all nodes $i$ with potential admissible out arcs. If a node $i$ does not have an admissible out arc, we remove it from $\text{LIST}$. Whenever we mark a node $j$, we add $j$ to $\text{LIST}$.

The full algorithm is given below:

Algorithm 6 Generic Search

procedure Search($G=(N,A),~s$)

unmark all nodes in $N$

mark node $s$

$\verb|pred|(s) := 0$

$\verb|next| := 1$

$\verb|order|(s) := 1$

$\verb|LIST|:=\{s\}$

while $\verb|LIST|\ne\emptyset$ do

select a node $i$ from $\verb|LIST|$

if node $i$ is incident to an admissible arc $(i,j)$ then

mark node $j$

$\verb|pred|(j) := i$

$\verb|next| := \verb|next|+1$

$\verb|order|(j) := \verb|next|$

add node $j$ to $\verb|LIST|$

else

delete node $i$ from $\verb|LIST|$

end if

end while

end procedure

The algorithm runs in $O(m+n)$ time.

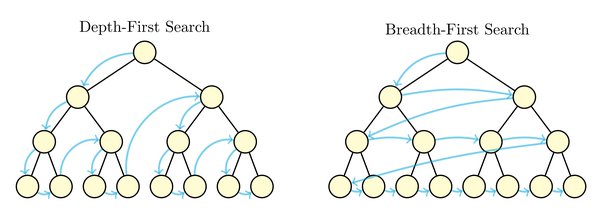
Breadth-First vs Depth-First Search

Depending on how we select nodes from $\text{LIST}$, we may get different search trees. If we maintain $\text{LIST}$ as a first-in, first-out (FIFO) queue, then we get breadth-first search (BFS). In BFS, we mark all admissible arcs $(i,j)$ that node $i$ is incident to before moving deeper into the tree.

Property. In the breadth-first search tree, the tree path from the source node $s$ to any node $i$ is a shortest path in terms of number of arcs.

If we instead maintain $\text{LIST}$ as a last-in, first out (LIFO) stack, then we get depth-first search (DFS). In this case, we move as deep as possible into the network first.

Property. In depth-first search, the following two properties hold:

1. If node $j$ is a descendant of node $i$ and $j\ne i$, then $\text{order}(j)>\text{order}(i)$.
2. All the descendants of any node are ordered consecutively in sequence.

Reverse Search

In reverse search, instead of starting at a source node and finding paths to each node $i\in N$, we instead start at a terminus node $t$ and find all paths from $i\in N$ to $t$. This can still be done with generic search with a couple tweaks. We initialize $\text{LIST}=\{t\}$ instead; while examining a node $i$, we look for incoming arcs of the node. Moreover, we now consider an arc $(i,j)$ admissible if $i$ is unmarked and $j$ is marked.