Relative Homology

A common tool in homology is relative homology, which is the homology of a space relative to subspace.

Let $K$ be a simplicial complex and $K_0\subset K$ a subcomplex. The relative p-chain group is then given by

$$C_p(K,K_0)=C_p(K)/C_p(K_0).$$

First notice that any chain $c\in C_p(K_0)$ is indeed a chain in $K$ as $K_0\subset K$; hence the quotient here is valid.

We can still construct the boundary map ${\partial }_p:C_p(K,K_0)\to C_{p-1}(K,K_0)$ by using the original homomorphism and inducing onto the quotient group:

$${\partial }_p[z]=[{\partial }_{p}z],\forall [z]\in C_p(K,K_0).$$

As a result we get the relative cycle group

$$Z_p(K,K_0)=\text{Ker}{\partial }_p$$

and relative boundary group

$$B_p(K,K_0)=\text{Im}{\partial }_p.$$

The relative homology group is then the quotient of quotients:

$$H_p(K,K_0)=Z_p(K,K_0)/B_p(K,K_0).$$

Example

Let $K$ be the annulus and $K_0\subset K$ be the right half.

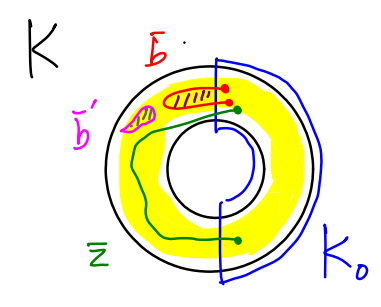
Notice that $z$ (green) is a 1-cycle in the quotient space $K/K_0$ which implies that $z\in Z_1(K,K_0)$. Likewise, $b$ (red) is a 1-boundary in $K/K_0$, i.e., $b\in B_1(K,K_0)$. Notice that $b^{\prime }$ (pink) is also a 1-boundary in $K/K_0$, but it is outside of $K_0$, so $b^{\prime }\in B_1(K,K_0)$ and $b^{\prime }\in B_1(K)$.

We view everything in $K_0$ as “trivial” in $K/K_0$. For example, if we look at $\partial z$, which is just the set of endpoints which are both in $K_0$. As a result, $\partial z$ is “trivial” in $K/K_0$. Hence, $z$ is a relative cycle.