Bracketing

Bracketing is the process of approximating the location of a local minimum by successively shrinking an interval around it. Many algorithms assume unimodality, i.e., there is a unique $x^{\ast }$ such that $f$ is monotonically decreasing for $x\le x^{\ast }$ and monotonically increasing for $x\ge x^{\ast }$. This unique point would then be a global minimum and no other local minima exist. The goal is then two find three points $a<b<c$ such that $f(a)>f(b)<f(c)$.

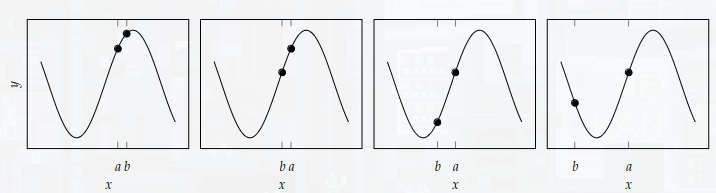
To find an initial bracket, we start at a given point we then step in the positive direction (the step distance is an example of a hyperparameter). Then we search in the downhill direction for the next point that exceeds the lowest point. We then repeat with a slightly larger step size. We stop once the $y$-value of the new point is greater than our initial point.

The full algorithm is given below:

def bracket_minimum(f, x=0, s=0.001, k=2):
	a, ya = x, f(x)
	b, yb = a + s, f(a+s)
	if yb > ya:
		a, b = b, a
		ya, yb = yb, ya
		s = -s
	while True:
		c, yc = b + s, f(b + s)
		if yc > yb:
			return (a,c) if a < c else (c,a)
		a, ya, b, yb = b, yb, c, yc
		s *= k

An example output:

Fibonacci and Golden Section Searches

Once we have bracketed a unimodal function $f$ by an interval $[a,b]$, we can perform Fibonacci search to maximally shrink the bracketed interval. By only evaluating $f$ twice, Fibonacci will remove 1/3 of the interval by evaluating at the 1/3 and 2/3 points along the interval. By moving the guesses towards the center of the interval, we get better results. Letting $|x_1-x_2|\to 0$ we shrink our interval by a factor of 2.

For $n$ evaluations, we can shrink our interval by a factor of $F_{n+1}$ where $F_n$ is the $n$-th Fibonacci number, i.e., the initial interval is $F_{n+1}$-times longer than the final interval.

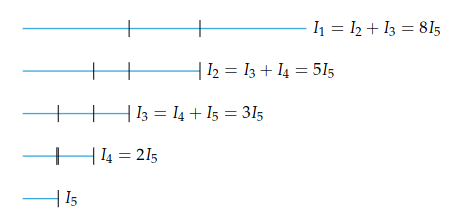The first two evaluations are made at

$$\begin{array}{rl}{x}_1& =a+(b-a)\left(1-\frac{F_n}{F_{n+1}}\right)\\ x_2& =a+(b-a)\frac{F_n}{F_{n+1}}.\end{array}$$

which ever has the lowest $y$-value becomes the new end point. We then repeat with $n-1$.

The algorithm is given below:

def fibonacci_search(f, a, b, n, eps=0.01):
	s = (1-sqrt(5)) / (1+sqrt(5))
	p = 1 / (GOLDEN_RATIO * (1-s**(n+1)) / (1 - s**n))
	d = p * b + (1-p) * a
	yd = f(d)
 
	for i in range(n):
		if i == n-1:
			c = eps * a + (1-eps)*d
		else:
			c = p*a + (1-p)*b
		yc = f(c)
		if yc < yd:
			b, d, yd = d, c, yc
		else:
			a, b = b, c
		p = 1 / (GOLDEN_RATIO * (1-s**(n-i)) / (1-s**(n-i-1)))
 
	return (a, b) if a < b else (b, a)

The ratio between successive Fibonacci numbers approaches the golden ratio,

$$\underset{n\to \infty }{\lim }\frac{F_n}{F_{n-1}}=\phi ,$$

for that reason it often easier to instead approximate the Fibonacci search using the golden ratio. That is, if the initial interval has length $I$, then the final interval should have length $I/{\phi }^{n-1}$. So we evaluate at

$$\begin{array}{rl}{x}_1& =a+(b-a)\left(1-\phi \right)\\ x_2& =a+(b-a)\phi .\end{array}$$

def golden_section_search(f, a, b, n):
	p = GOLDEN_RATIO - 1
	d = p * b + (1-p) * a
	yd = f(d)
	for i in range(n):
		c = p * a + (1-p) * b
		yc = f(c)
		if yc < yd:
			b, d, yd = d, c, yc
		else:
			a, b = b, c
 
	return (a,b) if a < b else (b, a)

Quadratic Fit Search

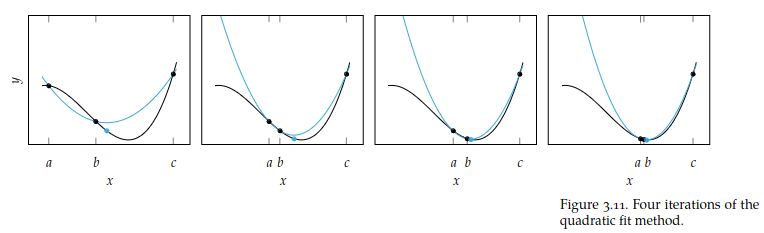
Often a curve appears quadratic near a local minima. Quadratic fit search attempts to solve for the minimum by fitting a quadratic curve to the function inside of our initial bracket.

Given bracket $a<b<c$ we wish to find the quadratic of the form

$$q(x)=p_1+p_{2}x+p_3{x}^2$$

that goes through $(a,y_a)$, $(b,y_b)$ and $(c,y_c)$. We can represent this problem in matrix form by

$$\left[\begin{array}{c}{y}_a\\ y_b\\ y_c\end{array}\right]=\left[\begin{array}{ccc}1& a& a^2\\ 1& b& b^2\\ 1& c& c^2\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right].$$

If the matrix is invertible, we can easily solve to get the quadratic function

$$q(x)=y_a\frac{(x-b)(x-c)}{(a-b)(a-c)}+y_b\frac{(x-a)(x-c)}{(b-a)(b-c)}+y_c\frac{(x-a)(x-b)}{(c-a)(c-b)}.$$

We then find the unique minimum of $q$ by finding the critical point. We then update our bracket with the minimum of $q$ and repeat the process until we reach our desired accuracy.

Bisection Method

The bisection method is designed to find roots of a function. We can use root-finding methods in optimization by applying them to the derivative of the objective function.

The bisection method starts with a bracket $[a,b]$ which we assume contains at least one root. If $f$ is continuous, then it follows by the intermediate value theorem, that if $f(a)$ and $f(b)$ have opposite signs, then there is some $c\in [a,b]$ such that $f(c)=0$.

In every iteration of the bisection method we cut the bracketed region in half. We evaluate the midpoint $(a+b)/2$ and replace the correct endpoint of our bracket so that the new bracket still has opposite signs. If the midpoint evaluates to zero, we terminate. Otherwise, we keep going until our desired accuracy or number of iterations.

def bisection_method(f, a, b, eps):
	ya, yb = f(a), f(b)
	while b-a > eps:
		c = (a+b) / 2
		fc = f(c)
		if fc == 0:
			a, b = c, c
		elif fc*fa > 0: # sgn(f(a)) = sgn(f(b))
			a = c
		else: # sgn(f(b)) = sgn(f(c))
			b = c
	return (a,b)

Of course we need our initial bracket to contain a sign change, i.e., $\text{sgn}(f(a))\ne \text{sgn}(f(b))$. A simple algorithm exists for choosing the initial bracket. We star with a guess interval. Then if the interval is invalid, we increase the interval width by a constant factor (often by 2). However, this method will not always work if the initial guess is too large.

Exercises

Exercise 3.1. Give an example of a problem when Fibonacci search is preferred over the bisection method.

Answer: Consider the following problem

$$\underset{x\in [0,1]}{\mathrm{minimize}}kx+c$$

where we are minimizing a linear function. Fibonacci search will give the correct answer, but bisection method uses the intermediate value theorem to find a root of the derivative. But in this case the derivative is constant and has no roots.

Exercise 3.4. For $f(x)=x^2/2-x$, apply the bisection method to find an interval containing the minimizer of $f$ starting with the interval $[0,1000]$. Execute three steps of the algorithm.

Answer: To use the bisection method we need to find a root of the derivative $f^{\prime }(x)$. Notice that

$$f^{\prime }(x)=x-1.$$

Clearly the minimizer is at $x=1$, but let’s apply the bisection method:

$a$	$b$	$c$	$f^{\prime }(a)$	$f^{\prime }(b)$	$f^{\prime }(c)$	$f(c)$
0	1000	500	-1	999	499	124500
0	500	250	-1	499	249	31000
0	250	125	-1	249	124	7687.5
After three steps we get the bracket $[0,125]$.

Exercise 3.6. Suppose we have a unimodal function defined on the interval $[1,32]$. After three function evaluations of our choice, will we be able to narrow the optimum to an interval of at most length 10? Why or why not?

Answer: Using only 3 function evaluations with Fibonacci search will only shrink the interval down by a factor of three giving us a new length of at most $10\frac{1}{3}$. If we have access to the functions derivative, then three evaluations would also only allow one step of bisection method ($f^{\prime }(1)$, $f^{\prime }(15.5)$, $f^{\prime }(32)$) which would give a new length of $16\frac{1}{2}$.

We could do a quadratic fit search, but we would only be able to do one iteration. Whether or not this would sufficiently shrink the interval depends on the function. In general, we cannot guarantee it would have a length of at most 10.