5. Manifolds

Recall that a topological space is second countable if it has a countable basis.

Topological Manifolds

Def

A topological space $M$ is locally Euclidean of dimension n if every point $p\in M$ has a neighborhood $U$ such that there is a homeomorphism $\varphi :U\to V\subset {\mathbb{R}}^n$. We call the pair $(U,\varphi )$ a chart, $U$ a coordinate neighborhood or coordinate open set and $\varphi$ a coordinate map or coordinate system on $U$.

Def

A topological manifold is a Hausdorff, second countable, locally Euclidean space.

Example: The Euclidean space ${\mathbb{R}}^n$ is covered by a single chart $({\mathbb{R}}^n,1_{{\mathbb{R}}^n})$. Hence ${\mathbb{R}}^n$ is an $n$-dimensional topological manifold.

Example: The graph of $y=x^{2/3}$ in ${\mathbb{R}}^2$ is a topological manifold. Since it is a subspace of ${\mathbb{R}}^2$, it is Hausdorff and second countable. The homeomorphism $(x,x^{2/3})\mapsto x$ shows that it is locally Euclidean.

Example: The two axes in ${\mathbb{R}}^2$ with the subspace topology is not a topological manifold due the intersection at the origin. Indeed, assume the axes were locally Euclidean at the origin. Then their is a neighborhood $U$ of the origin homeomorphic to an open ball $B(0,ϵ)\subset {\mathbb{R}}^2$. Notice that $U\setminus \{0\}$ has four connected components, whereas $B(0,ϵ)\setminus \{0\}$ has one. Therefore, they are not homeomorphic.

In order for the definition of manifold to be well defined, we need to ensure that every neighborhood is homeomorphic to a open set in ${\mathbb{R}}^n$ for the same degree $n$. This is known as the invariance of dimension and is true.

Compatible Charts

Let $(U,\varphi )$ and $(V,\psi )$ be charts. Since $U$ and $V$ are open, it follows that $U\cap V$ is open. Moreover, since $\varphi$ and $\psi$ are homeomorphisms, it follows that $\varphi (U\cap V)$ and $\psi (U\cap V)$ are open.

Def

Two charts $(U,\varphi )$ and $(V,\psi )$ are $C^{\infty }$-compatible if the two transition maps

$$\varphi \circ {\psi }^{-1}:\psi (U\cap V)\to \varphi (U\cap V),\psi \circ {\varphi }^{-1}:\varphi (U\cap V)\to \psi (U\cap V)$$

are $C^{\infty }$. If the two charts do not intersect, they are automatically $C^{\infty }$-compatible.

Some authors use $U_{\alpha \beta }$ for $U_{\alpha }\cap U_{\beta }$.

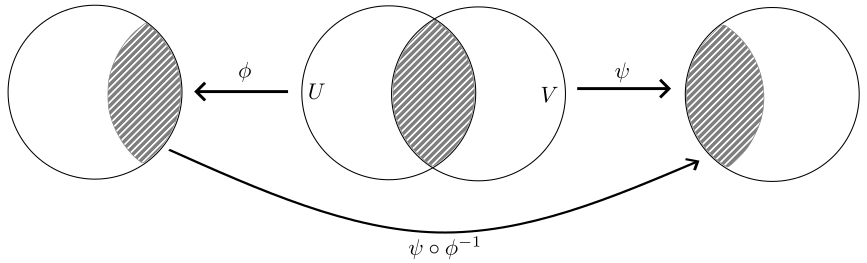
Def

A $C^{\infty }$ atlas on a locally Euclidean space $M$ is a collection $\mathfrak{U}=\{(U_{\alpha },{\varphi }_{\alpha })\}$ of pairwise $C^{\infty }$-compatible charts that cover $M$, i.e., $M={\bigcup }_{\alpha }{U}_{\alpha }$.

Example: The unit circle can be viewed as the complex subset

$$S^1=\{e^{it}\in \mathbb{C}\mid 0\le t\le 2\pi \}.$$

Define the two open subsets

$$\begin{array}{rl}{U}_1& =\{e^{it}\in \mathbb{C}\mid -\pi <t<\pi \}\\ U_2& =\{e^{it}\in \mathbb{C}\mid 0<t<2\pi \}.\end{array}$$

Define the coordinate maps

$$\begin{array}{rlr}{\varphi }_1(e^{it})& =t,& -\pi <t<\pi \\ {\varphi }_2(e^{it})& =t,& 0<t<2\pi \end{array}$$

One may show that $(U_1,{\varphi }_1)$ and $(U_2,{\varphi }_2)$ are charts on $S^1$. The intersection $U_1\cap U_2$ consists of two connected components:

$$\begin{array}{rl}A& =\{e^{it}\in \mathbb{C}\mid -\pi <t<0\}\\ B& =\{e^{it}\in \mathbb{C}\mid 0<t<\pi \}\end{array}$$

and

$$\begin{array}{rl}{\varphi }_1(U_1\cap U_2)& ={\varphi }_1(A\cup B)=(-\pi ,0)\cup (0,\pi )\\ {\varphi }_2(U_1\cap U_2)& ={\varphi }_2(A\cup B)=(\pi ,2\pi )\cup (0,\pi )\end{array}$$

The transition maps are given by

$$({\varphi }_2\circ {\varphi }_1^{-1})(t)=\{\begin{array}{ll}t+2\pi & \text{if }t\in (-\pi ,0)\\ t& \text{if }t\in (0,\pi )\end{array}$$

and

$$({\varphi }_1\circ {\varphi }_2^{-1})(t)=\{\begin{array}{ll}t-2\pi & \text{if }t\in (\pi ,2\pi )\\ t& \text{if }t\in (0,\pi ).\end{array}$$

Therefore, $(U_1,{\varphi }_1)$ and $(U_2,{\varphi }_2)$ form a $C^{\infty }$ atlas on $S^1$.

$C^{\infty }$-compatible is not an equivalence relation. While it is reflexive and symmetric, it is not necessarily transitive.

We say a chart $(V,\psi )$ is compatible with an atlas $\{(U_{\alpha },{\varphi }_{\alpha })\}$ if it is compatible with all the charts $(U_{\alpha },{\varphi }_{\alpha })$ of the atlas.

Lemma

Let $\{(U_{\alpha },{\varphi }_{\alpha })\}$ be an atlas on a locally Euclidean space. If two charts $(V,\psi )$ and $(W,\sigma )$ are both compatible with the atlas, then they are compatible with each other.

Proof: Let $p\in V\cap W$. Note there is some $\alpha$ such that $p\in U_{\alpha }$. Thus, $p\in V\cap W\cap U_{\alpha }$. So

$$\sigma \circ {\psi }^{-1}=(\sigma \circ {\varphi }_{\alpha }^{-1})\circ ({\varphi }_{\alpha }\circ {\psi }^{-1})$$

is $C^{\infty }$ on $V\cap W\cap U_{\alpha }$. This holds for all $p\in V\cap W$. Therefore, $\sigma \circ {\psi }^{-1}$ is $C^{\infty }$ on $V\cap W$. A similar argument holds for $\psi \circ {\sigma }^{-1}$.

Q.E.D.

Smooth Manifolds

An atlas is considered maximal if it is not contained in a larger atlas.

Def

A smooth or $C^{\infty }$-manifold is a topological manifold $M$ together with a maximal atlas. The maximal atlas is called a differentiable structure on $M$.

In practice, one only needs to find any atlas to show a topological manifold is a smooth manifold.

Prp

Any atlas $\mathfrak{U}=\{(U_{\alpha },{\varphi }_{\alpha })\}$ on a locally Euclidean space is contained in a unique maximal atlas.

Proof: Adjoin all charts $(V_i,{\psi }_i)$ that are compatible with $\mathfrak{U}$. The resulting atlas is maximal and unique.

Q.E.D.

To show a topological space $M$ is a smooth manifold it suffices to check that

1. $M$ is Hausdorff and second countable
2. $M$ has a $C^{\infty }$ atlas.

Let $r^1,\dots ,r^n$ be the standard coordinates on ${\mathbb{R}}^n$. For a chart $(U,\varphi )$ we let $x^i=r^i\circ \varphi$ be the $i$-th component of $\varphi$ and write $(U,\varphi )=(U,x^1,\dots ,x^n)$. We call the functions $x^1,\dots ,x^n$ coordinates or local coordinates on $U$.

Examples of Smooth Manifolds

Example: The Euclidean space ${\mathbb{R}}^n$ is a smooth manifold with the chart $({\mathbb{R}}^n,r^1,\dots ,r^n)$ where $r^1,\dots ,r^n$ are the standard coordinates on ${\mathbb{R}}^n$.

Example: Any open subset $V$ of a manifold $M$ is also a manifold under the subspace topology. Let $\{(U_{\alpha },{\varphi }_{\alpha })\}$ be an atlas for $M$, and notice that $\{(U_{\alpha }\cap V,{\varphi }_{\alpha }{|}_{U_{\alpha }\cap V})\}$ forms an atlas for $V$.

Example: In a manifold of dimension zero, every singleton subset is homeomorphic to ${\mathbb{R}}^0$ and hence open. So every zero-degree manifold is a discrete set.

Example: For a subset $A\subset {\mathbb{R}}^n$ and function $f:A\to {\mathbb{R}}^m$, we define the graph of $f$ to be the subset

$$\Gamma (f)=\{(x,f(x))\in A\times {\mathbb{R}}^m\}.$$

Consider an open subset $U\subset {\mathbb{R}}^n$ and assume that $f$ is $C^{\infty }$ on $U$. Then the map

$$\varphi :\Gamma (f)\to U,(x,f(x))\mapsto x$$

and the map

$$(1,f):U\to \Gamma (f),x\mapsto (x,f(x))$$

are continuous and inverses of each other. Hence, they are homeomorphisms. Therefore, the graph of a $C^{\infty }$ function $f:U\to {\mathbb{R}}^m$ is a $C^{\infty }$ manifold with the atlas comprised of a single chart, $(\Gamma (f),\varphi )$.

Example: Notice that ${\mathbb{R}}^{m\times n}$ is isomorphic to ${\mathbb{R}}^{mn}$. Hence we can give the topology of ${\mathbb{R}}^{mn}$ to ${\mathbb{R}}^{m\times n}$. The general linear group is the set of invertible matrices:

$$\text{GL}(n,\mathbb{R}):=\{A\in {\mathbb{R}}^{n\times n}\mid \det A\ne 0\}={\text{det}}^{-1}({\mathbb{R}}^{\setminus }\{0\}).$$

Since $\det :{\mathbb{R}}^{n\times n}\to \mathbb{R}$ is continuous, the general linear group is an open subset of ${\mathbb{R}}^{n\times n}$. Therefore, it is a manifold of dimension $n^2$ by our second example.

By similar reasoning, the complex general linear group $\text{GL}(n,\mathbb{C})$ is also a manifold of dimension $2n^2$.

Prp

If $\{(U_{\alpha },{\varphi }_{\alpha })\}$ and $\{(V_{\beta },{\psi }_{\beta })\}$ are $C^{\infty }$ atlases for manifolds $M$ and $N$ of dimensions $m$ and $n$, respectively, then the collection

$$\{(U_{\alpha }\times V_{\beta },{\varphi }_{\alpha }\times {\psi }_{\beta })\}$$

of charts is a $C^{\infty }$ atlas on $M\times N$. Therefore, $M\times N$ is a manifold of dimension $m+n$.

Proof: Recall that the product of Hausdorff spaces are Hausdorff. Moreover, the product of second countable spaces are second countable. Hence we simply show that the above collection forms a $C^{\infty }$ atlas.

Let $(U_{{\alpha }_1}\times V_{{\beta }_1},{\varphi }_{{\alpha }_1}\times {\psi }_{{\beta }_1})$ and $(U_{{\alpha }_2}\times V_{{\beta }_2},{\varphi }_{{\alpha }_2}\times {\psi }_{{\beta }_2})$ be overlapping charts. Notice that

$$\begin{array}{rl}(({\varphi }_{{\alpha }_1}\times {\psi }_{{\beta }_1})\circ ({\varphi }_{{\alpha }_2}\times {\psi }_{{\beta }_2}{)}^{-1})(x,y)& =({\varphi }_{{\alpha }_1}\times {\psi }_{{\beta }_1})({\varphi }_{{\alpha }_2}^{-1}(x),{\psi }_{{\beta }_2}^{-1}(y))\\ & =(({\varphi }_{{\alpha }_1}\circ {\varphi }_{{\alpha }_2}^{-1})(x)),({\psi }_{{\beta }_1}\circ {\psi }_{{\beta }_2}^{-1})(y)).\end{array}$$

Since $\{(U_{\alpha },{\varphi }_{\alpha })\}$ is an atlas for $M$, ${\varphi }_{{\alpha }_1}\circ {\varphi }_{{\alpha }_2}^{-1}$ is $C^{\infty }$. Likewise, ${\psi }_{{\beta }_1}\circ {\psi }_{{\beta }_2}^{-1}$ is $C^{\infty }$. Therefore, the product of the two is $C^{\infty }$. An identical argument holds for the opposite transition map.

Therefore, $M\times N$ is a manifold of dimension $m+n$.

Q.E.D.

Example: As a consequence of the previous proposition, the infinite cylinder $S^1\times \mathbb{R}$ and the torus $S^1\times S^1$ are smooth manifolds. Moreover, the $n$-dimensional torus $S^1\times \cdots \times S^1$ is also a manifold.

For dimensions less than 4, every topological manifold has a unique differentiable structure. In dimensions greater than 4, every compact topological manifold has a finite number of differentiable structures. Nothing is known about dimension 4.

Smooth Poincare conjecture

$S^4$ has a unique differentiable structure.

As shown by Michel Kervaire, there exists topological manifolds with no differentiable structure, i.e., there are topological manifolds that are not $C^{\infty }$.

Problems