Reduced Homology

There is an issue needing addressing for Smith normal form when $p=0$. Recall our complex $K$:

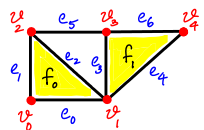
If we look at the boundary matrix $[{\partial }_0]$, then

$$\text{SNF}([{\partial }_0])=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\end{array}\right]$$

which suggest the Betti number is ${\beta }_0=z_0-b_0=4-4=0$. But, this contradicts with our notion of ${\beta }_0$ representing the number of connected components. To correct this, we add the augmentation map $ϵ:C_0\to {\mathbb{Z}}_2$ defined by $ϵ(v_j)=1$ to our chain complex:

$$\cdots \stackrel{{\partial }_2}{\to }{C}_1\stackrel{{\partial }_1}{\to }{C}_0\stackrel{ϵ}{\to }{\mathbb{Z}}_2\stackrel{0}{\to }0$$

Notice that we still get that $ϵ\circ {\partial }_1=0$ since each edge has two vertices:

$$ϵ({\partial }_1(v_i{v}_j))=ϵ(v_i+v_j)=1+1=0.$$

Under this new chain complex, we get the reduced homology groups $\widetilde{H_p}$ as well as the reduced Betti numbers $\widetilde{{\beta }_p}$.

Reduced Homology Groups

The p-th reduced homology group is given by

$$\widetilde{H_p}=\{\begin{array}{ll}{Z}_p/B_p& \text{if }p>0\\ \text{Ker}(ϵ)/B_0& \text{if }p=0.\end{array}$$

For $p>0$, the reduced homology group and homology group coincide.

Reduced Betti numbers

The p-th reduced Betti number is given by

$$\widetilde{{\beta }_p}=\text{rank}\widetilde{H_p}$$

Alternatively,

$$\widetilde{{\beta }_p}=\{\begin{array}{ll}{\beta }_p& \text{if }p>0\\ {\beta }_0-1& \text{if }p=0.\end{array}$$

Remark: When working over $\mathbb{Z}$, the augmentation map $ϵ:C_0\to \mathbb{Z}$ is defined the same, $ϵ(v_j)=1$.