Median shapes

Authors: Yunfeng Hu, Matthew Hudelson, Bala Krishnamoorthy, Altansuren Tumurbaatar and Kevin Vixie.

Full paper can be found at https://jocg.org/index.php/jocg/article/view/3078.

---

Introduction

The authors suggest the textbook Geometric Measure Theory: A Beginner’s Guide for an introduction to geometric measure theory.

Shapes as Currents

A $p$-current in ${\mathbb{R}}^d$ is any element of the dual space of smooth, compactly supported $p$-forms in ${\mathbb{R}}^d$ (so a linear functional mapping $p$-forms to $\mathbb{R}$). Intuitively, one may view them as a union of a finite number of pieces of oriented $p$-dimensional smooth manifolds in ${\mathbb{R}}^d$ with an orienting $p$-vector field on the submanifolds.

A Hausdorff measure of a set $E\subset {\mathbb{R}}^n$ is defined using efficient covers of $E$. Intuitively, ${\mathcal{H}}^p(E)$ is the $p$-dimensional volume of $E$; we compute it as

$${\mathcal{H}}^p(E)=\underset{\delta \to 0}{\lim }\underset{C_{\delta }}{\inf }\sum \alpha (p){\left(\frac{\text{diam}(C_i)}{2}\right)}^p$$

where the $C_{\delta }$‘s are the collections of sets $\{C_i{\}}_i^{\infty }$ such that $E\subset {\bigcup }_i{C}_i$ and $\text{diam}{C}_i<\delta$, and $\alpha (p)$ is the volume of the unit ball in ${\mathbb{R}}^p$.

Remark: In ${\mathbb{R}}^d$, ${\mathcal{H}}^d={\mathcal{L}}^d$, i.e., the Hausdorff measure is the same as the Lebesgue measure.

Rectifiable set

A set $E$ is a $p$-rectifiable subset of ${\mathbb{R}}^d$ if

$$E\subset \left\{\bigcup _i{f}_i({\mathbb{R}}^p)\cup N_0\right\}$$

where each of the $f_i:{\mathbb{R}}^p\to {\mathbb{R}}^d$ are Lipschitz, and the $p$-Hausdorff measure ${\mathcal{H}}^p(N_0)=0$.

Rectifiable Currents

We say $R$ is a rectifiable current if there is a $p$-vector field $\zeta (x)$ in ${\mathbb{R}}^d$, an integer valued function $m:{\mathbb{R}}^d\to \mathbb{Z}$, and a rectifiable set $E$ with ${\int }_E|m(x)|d{\mathcal{H}}^{p}x<\infty$ such that for any $p$-form $\omega$,

$$R(\omega )={\int }_{E}m(x)\omega (\zeta (x))d{\mathcal{H}}^{p}x.$$

Based on figure 3, it seems a rectifiable current is obtained by orienting a rectifiable set. The boundary of a $p$-current $T$ is then the $(p-1)$-current $\partial T$ given by

$$\partial T(\omega ):=T(d\omega )$$

where $d\omega$ denotes the exterior derivative of the $(p-1)$-form $\omega$.

The Multiscale Flat Norm

Given a $p$-current $H$, we decompose $H$ into two components: $H=(H-\partial S)+(\partial S)$ where $S$ is any $(p+1)$-current. Then the flat norm of $H$ is given by the current $S$ that results in the smallest mass, i.e.,

$$\mathbb{F}(H)=\underset{S\in {\mathcal{D}}^{p+1}}{\inf }M(H-\partial S)+M(S)$$

where ${\mathcal{D}}^{p+1}$ is the space of $(p+1)$-currents and

$$M(T)=\underset{\omega }{\sup }\{T(\omega ):\Vert \omega (x)\Vert \le 1\text{ almost everywhere}\}$$

is the mass of a current $T$.

The multiscale flat norm is a simple generalization of the flat norm given by

$${\mathbb{F}}_{\lambda }(H)=\underset{S\in {\mathcal{D}}^{p+1}}{\inf }M(H-\partial S)+\lambda M(S),\text{for }\lambda \ge 0.$$

Means and Medians in the Space of Integral Currents

Given a set of integral $p$-currents $\{T_i\}$, we define their mean as

$$\overline{T}=\arg \underset{T\in {\mathcal{I}}^p}{\min }\sum _i{\mathbb{F}}_{\lambda }(T-T_i{)}^2$$

and their median as

$$\hat{T}=\arg \underset{T\in {\mathcal{I}}^p}{\min }\sum _i{\mathbb{F}}_{\lambda }(T-T_i)$$

where ${\mathcal{I}}^p$ is the set of all integral $p$-currents. We are also interested in the mass regularized version of the mean and median:

$$\begin{array}{rl}{\overline{T}}_{\mu }& =\arg \underset{T\in {\mathcal{I}}^p}{\min }\sum _i{\mathbb{F}}_{\lambda }(T-T_i{)}^2+\mu M(T)\text{ for }\mu \ge 0\\ {\hat{T}}_{\mu }& =\arg \underset{T\in {\mathcal{I}}^p}{\min }\sum _i{\mathbb{F}}_{\lambda }(T-T_i)+\mu M(T)\text{ for }\mu \ge 0.\end{array}$$

The median $\hat{T}$ can be computed efficiently by a linear optimization problem.

Median Shapes on Simplicial Complexes: Preliminaries

We know represent integral $p$-currents as $p$-chains in a simplicial complex $K$ of dimension $q\ge p+1$. More specifically, the case in which $K$ is a finite simplicial complex.

Let ${\sigma }_i$, $i=1,\dots ,m$, denote the $p$-simplices and ${\tau }_j$, $j=1,\dots ,n$, denote the $(p+1)$-simplices of $K$. To find the simplicial flat norm of the integral current represented by the $p$-chain

$$\text{t}=\sum _i{t}_i{\sigma }_i$$

with underlying group $t_i\in \mathbb{Z}$, we look for candidate $(p+1)$-chains

$$\text{s}=\sum _j{s}_j{\tau }_j$$

which defines the decomposition as

$$\text{x}=\sum _i{x}_i{\sigma }_i=\text{t}-{\partial }_{p+1}\text{s}.$$

Note then that $\text{x}$ and $\text{t}$ are homologous $p$-chains. The flat norm decomposition is then given by the pair of chains $(\text{x},\text{s})$ which minimizes the sum of weighted volumes of these chains, i.e.,

$$\underset{\text{x},\text{s}}{\mathrm{minimize}}\sum _{i=1}^m{V}_p({\sigma }_i)|x_i|+\lambda \sum _{j=1}^n{V}_{p+1}({\tau }_j)|s_j|,$$

where $V_p(\sigma )$ is the $p$-dimensional volume of simplex $\sigma$. The volume $V_p(\sigma )$ is equivalent to the mass $M(\sigma )$ of the $p$-simplex $\sigma$. Therefore, we may define the multiscale flat norm for a simplicial complex $p$-chain $\text{t}\in C_p(K)$ as

$${\mathbb{F}}_{\lambda }(\text{t})=\underset{\text{x}\in C_p(K),\text{s}\in C_{p+1}(K)}{\min }\left\{\sum _{i=1}^m{V}_p({\sigma }_i)|x_i|+\lambda \sum _{j=1}^n{V}_{p+1}({\tau }_j)|s_j||\text{x}=\text{t}-{\partial }_{p+1}\text{s}\right\},\text{for }\lambda \ge 0.$$

Recall that we can capture the boundary operator ${\partial }_{p+1}$ by the $(p+1)$-boundary matrix $B=[{\partial }_{p+1}]$ of $K$ where $B_{ij}=\pm 1$ when ${\sigma }_i⪯{\tau }_j$ and $B_{ij}=0$ otherwise. More specifically, $B_{ij}=1$ indicates that ${\sigma }_i⪯{\tau }_j$ and they have the same orientation.

Simplicial Median Shape and Integer Linear Optimization

The authors view the median shape problem in terms of simplices and present and IP for the simplicial median shape problem. Since the homology groups are over $\mathbb{Z}$, we insist on integral solutions. Even though the IP is not unimodular, the LP relaxation of the IP has always provided integral solutions in practice.

Median Shape as an Integer Program

Let $C_p(K)$ denote the group of $p$-chains of the simplicial complex $K$. We view a set of $N$ currents as $p$-chains $t_1,t_2,\dots ,t_N\in C_p(K)$. Then the simplicial median shape $\hat{\text{t}}$ is the $p$-chain $\text{t}\in C_p(K)$ in which

$$\sum _{h=1}^N\rho (\text{t},{\text{t}}_h)=\sum _{h=1}^N{\mathbb{F}}_{\lambda }(\text{t}-{\text{t}}_h)$$

is minimized, i.e.,

$$\begin{array}{rl}\hat{\text{t}}& =\underset{\text{t}\in C_p(K)}{\mathrm{argmin}}\sum _{h=1}^N{\mathbb{F}}_{\lambda }(\text{t}-{\text{t}}_h).\end{array}$$

Denote by ${\text{r}}_h\in C_p(K)$ and ${\text{s}}_h\in C_{p+1}(K)$ a potential flat norm decomposition of $\text{t}-{\text{t}}_h$, i.e., $\text{t}-{\text{t}}_h={\text{r}}_h+{\partial }_{p+1}{\text{s}}_h$. Denote by $r_{hi}$ the $i$-th component of ${\text{r}}_h$. Denote the volumes by $V_p({\sigma }_i)=w_i$ and $V_{p+1}({\tau }_j)=v_j$. Then the median shape problem can be viewed as the following optimization problem:

$$\begin{array}{rlr}\text{minimize}& \sum _{h=1}^N\left(\sum _{i=1}^m{w}_i|r_{hi}|+\lambda \sum _{j=1}^n{v}_j|s_{hj}|\right)& \\ \text{subject to}& \text{t}-{\text{t}}_h={\text{r}}_h+{\partial }_{p+1}{\text{s}}_h& h=1,2,\dots ,N,\\ & \text{t}\in {\mathbb{Z}}^m,{\text{r}}_h\in {\mathbb{Z}}^m,{\text{s}}_h\in {\mathbb{Z}}^n& h=1,2,\dots ,N.\end{array}$$

Note that ${\partial }_{p+1}{\text{s}}_h$ is given by the matrix product $B{\text{s}}_h$, where $B$ is the $(p+1)$-boundary matrix of $K$, and hence linear. However, $|r_{hi}|$ and $|s_{hj}|$ is not linear. We fix this by splitting each the parameters ${\text{r}}_h$ and ${\text{s}}_h$ into two terms each such that

$${\text{r}}_h={\text{r}}_h^{+}-{\text{r}}_h^{=}\text{ and }{\text{s}}_h={\text{s}}_h^{+}-{\text{s}}_h^{-}.$$

Under this transformation, we now get an IP:

$$\begin{array}{rlr}\text{minimize}& \sum _{h=1}^N\left(\sum _{i=1}^m{w}_i(r_{hi}^{+}+r_{hi}^{-})+\lambda \sum _{j=1}^n{v}_j(s_{hj}^{+}+s_{hj}^{-})\right)& \\ \text{subject to}& \text{t}-{\text{t}}_h=({\text{r}}_h^{+}-{\text{r}}_h^{-})+{\partial }_{p+1}({\text{s}}_h^{+}-{\text{s}}_h^{-})& h=1,2,\dots ,N,\\ & {\text{r}}_h^{+},{\text{r}}_h^{-}\ge 0,{\text{s}}_h^{+},{\text{s}}_h^{-}\ge 0& h=1,2,\dots ,N,\\ & \text{t}\in {\mathbb{Z}}^m,{\text{r}}_h^{+},{\text{r}}_h^{-}\in {\mathbb{Z}}^m,{\text{s}}_h^{+},{\text{s}}_h^{-}\in {\mathbb{Z}}^n& h=1,2,\dots ,N.\end{array}$$

See the paper (page 54) for the IP in matrix form.

Total Unimodularity and the Median Shape LP

We relax the IP to an LP by ignoring the integrality constraints.

Totally Unimodular

A totally unimodular matrix is an integral matrix for which every square submatrix has determinant $0$, $+1$, or $-1$.

TU is preserved under the following operations.

1. Permuting rows or columns.
2. Taking the transpose.
3. Multiplying a row or column by $\pm 1$.
4. Adding a row or column of all zeros, or adding a row or column with one nonzero that is $\pm 1$.
5. Repeating a row or column.

Def

The $N$-fold $I$-sum of an $m\times n$ matrix $A$ is the $(mN+n)\times nN$ matrix

$${\boxed{I}}_{N}A:=\left[\begin{array}{cccc}I& I& \cdots & I\\ A& & & \\ & A& & \\ & & \ddots & \\ & & & A\end{array}\right].$$

Remark: The $N$-fold $I$-sum is denoted by a $I$ in a circle. There does not appear to be a way to write this in $\text{LATEX}$ without tikz. In my notes I will use a box.

While the $N$-sum $A\oplus A\oplus A\oplus \cdots \oplus A$ preserve TU, the $N$-fold $I$-sum does not.

Generalizations of the Median Shape LP

We can modify the median shape LP to find a median shape with mass regularization, by replacing $\text{t}$ with ${\text{t}}^{+}-{\text{t}}^{-}$ and adding $\mu {\text{w}}^{\top }({\text{t}}^{+}+{\text{t}}^{-})$ to the objective function. We require that $\mu \ge 0$, and typically $\mu <\lambda$.

One could also take the generalized weighted simplicial median shape problem which seeks $\text{t}\in C_p(K)$ that minimizes

$$\sum _{h=1}^N{\alpha }_h{\mathbb{F}}_{\lambda }(\text{t}-{\text{t}}_h),\text{ where }\sum _{h=1}^N{\alpha }_h=1\text{ and }{\alpha }_h\in [0,1].$$

Complexity of Simplicial Median Shape

We wish to analyze the computational complexity of the mass-regularized weighted simplicial median shape problem (MRWSMSP). We consider the decision version of the MRWSMSP to get the DMRWSMSP.

Consider $N$ input $p$-chains ${\text{t}}_1,\dots ,{\text{t}}_N$, $p$-chain $\text{t}$, and $N$ pairs of $p$ and $(p+1)$-chains $({\text{r}}_1,{\text{s}}_1),\dots ,({\text{r}}_N,{\text{s}}_N)$ such that $\text{t}-{\text{t}}_h={\text{r}}_h+{\partial }_{p+1}{\text{s}}_h$. Then given weights $\alpha =[{\alpha }_1,\cdots ,{\alpha }_N]\ge 0$ and parameters $\lambda ,\mu \ge 0$ we define the function

$$\begin{array}{rl}{f}_{\alpha ,\lambda ,\mu }(\text{t},{\text{t}}_1,\dots ,{\text{t}}_N)& =\mu \sum _{i=1}^m{w}_i|t_i|\\ & +{\alpha }_1\left(\sum _{i=1}^m{w}_i|r_{1i}|+\lambda \sum _{j=1}^n{v}_j|s_{1j}|\right)+\cdots \\ & +{\alpha }_N\left(\sum _{i=1}^m{w}_i|r_{Ni}|+\lambda \sum _{j=1}^n{v}_j|s_{Nj}|\right).\end{array}$$

Then the DMRWSMSP can be viewed as whether there is an input in which $f_{\alpha ,\lambda ,\mu }(\text{t},{\text{t}}_1,\dots ,{\text{t}}_N)\le f_0$ where $f_0\ge 0$ is some given rational number.

Lemma

DMRWSMSP is NP-complete and MRWSMSP is NP-hard.

A special case of DMRWSMSP is the optimal homologous chain problem (OHCP) which seeks to find a chain with the minimal total weight in the same homology class as the input chain in a finite simplicial complex. That is, DMRWSMSP with a single input chain gives the OHCP.

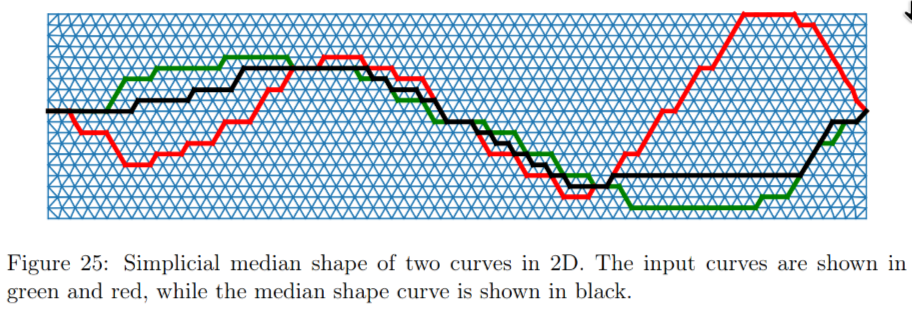
Computational Experiments

In the figure below is a simple mesh with 3851 edges and 2510 triangles. There are two input 1-chains (green and red). The authors chose $\lambda =10^{-3}$ and $\mu =10^{-5}$. The mass-regularized median shape is shown in black.

Full code: https://github.com/tbtraltaa/medianshape