Duality

The Dual Problem

Every optimization can be viewed in two ways: the primal or the dual. For example, if the primal LP is

$$\begin{array}{rlr}& \text{maximize}& z=\sum _{j=1}^n{c}_j{x}_j\\ & \text{subject to}& \sum _{j=1}^n{a}_{ij}{x}_j\le b_i,\forall i=1,2,\dots ,m\\ & & x_j\ge 0,\forall j=1,2,\dots ,n\end{array}$$

then it’s dual is

$$\begin{array}{rlr}& \text{minimize}& v=\sum _{i=1}^m{b}_i{y}_i\\ & \text{subject to}& \sum _{i=1}^m{y}_i{a}_{ij}\ge c_j,\forall j=1,2,\dots ,n\\ & & y_i\ge 0,\forall i=1,2,\dots ,m.\end{array}$$

The variables $c$ and $b$ switch places with each other; the coefficients $c_j$ become the right-hand side of the dual and right-hand side of the primal ($b_j$) becomes the coefficients of the dual.

In summary:

$$\begin{array}{rlrlrlr}& \text{maximize}& z=c^{\top }x& & & \text{minimize}& v=b^{\top }y\\ & \text{subject to}& Ax\le b& ⟷& & \text{subject to}& A^{\top }x\ge c\\ & & x\ge 0& & & & y\ge 0\end{array}$$

Properties

As you choose values of $x$ or $y$ that come closer to the optimal solution, the optimal values $z$ and $v$ for the primal and dual, respectively converge towards the shared optimal solution from opposite directions.

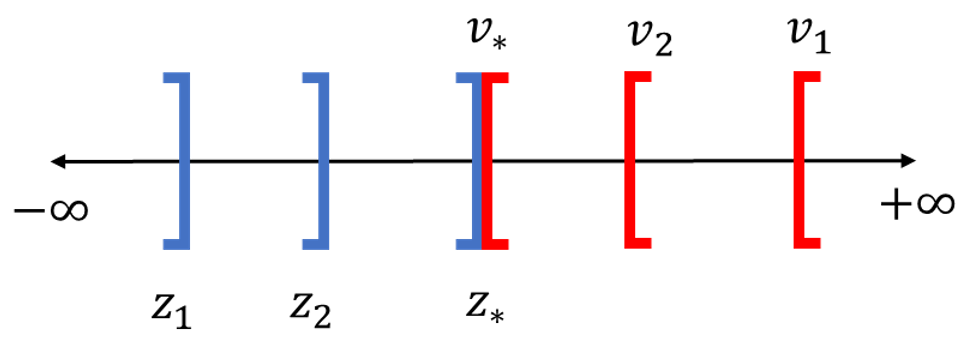
Weak Duality

Let $x$ be any feasible solution to the primal and $y$ be any feasible solution to the dual. Then

$$z=c^{\top }x\le b^{\top }y=v.$$

In other words, the primal problem converges from below and the dual problem converges from above.

Strong Duality

Let $x$ be a feasible solution to the primal and $y$ a feasible solution to the dual. Then if

$$z=c^{\top }x=b^{\top }y=v$$

then $x$ is optimal for the primal and $y$ is optimal for the dual.

As a result, if the primal has an optimal solution $x^{\ast }$ and the dual has an optimal solution $y^{\ast }$, then $c^{\top }{x}^{\ast }=b^{\top }{y}^{\ast }$.

Example

Consider the following LP:

$$\begin{array}{rlr}& \text{maximize}& z=6x_1+14x_2+13x_3\\ & \text{subject to}& \frac{1}{2}{x}_1+2x_2+x_3\le 24\\ & & x_1+2x_2+4x_3\le 60\\ & & 3x_1+5x_3\le 12\end{array}$$

Rewriting the constraints in the form $Ax\le b$ has the matrix

$$A=\left[\begin{array}{ccc}\frac{1}{2}& 2& 1\\ 1& 2& 4\\ 3& 0& 5\end{array}\right].$$

Therefore, the dual LP is

$$\begin{array}{rlr}& \text{maximize}& z=24y_1+60y_2+12y_3\\ & \text{subject to}& \frac{1}{2}{y}_1+y_2+3y_3\ge 6\\ & & 2y_1+2y_2\ge 14\\ & & y_1+4y_2+5y_3\ge 13\end{array}$$