Maximum Flow

The goal of maximum flow problems is send as much flow as possible from node $s$ to node $t$ without exceeding arc capacities. Mathematically we can view this as the optimization problem

$$\begin{array}{rlr}& \text{maximize}& v\\ & \text{subject to}& \sum _{(i,j)\in A}{x}_{ij}-\sum _{(j,i)\in A}{x}_{ji}=\{\begin{array}{ll}v& \text{if }i=s\\ 0& \text{if }i\in N\setminus \{s,t\}\\ -v& \text{if }i=t\end{array}\\ & & 0\le x_{ij}\le u_{ij},\forall (i,j)\in A.\end{array}$$

where $v$ is the value of flow. For example, consider the flow along the network below:

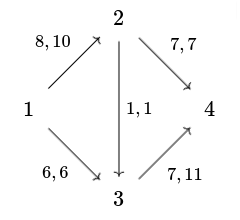
Where $s=1$, $t=4$ and arcs $(i,j)\in A$ are labeled $x_{ij},u_{ij}$. Here the value of flow is

$$v=8+6=7+7=14.$$

In maximum flow we make the following assumptions:

1. $G=(N,A)$ is directed.
2. All capacities $u_{ij}$ are non-negative integers.
3. $G$ does not contain a directed $s-t$ path $P$ with $u_{ij}=\infty$ for all $(i,j)\in P$.
4. When $(i,j)\in A$, $(j,i)$ is also present in $A$. (One may correct this by adding $(j,i)$ with $u_{ji}=0$).
5. There are no parallel (forward) arcs. If such arcs are present, we add extra node(s) to split all but one of them.

Feasibility Problem

In a feasibility problem we seek a feasible flow in $G=(N,A)$ with $b(i)$ and $u_{ij}$ such that $\sum b(i)=0$. For example consider a simple transportation problem on node sets $N_1\cup N_2$. We add nodes $s,t$, arcs $(s,i)$ with $u_{si}=b(i)$ for all $i\in N_1$ and arcs $(j,t)$ with $u_{jt}=-b(j)$ for all $j\in N_2$. If the maximum flow saturates all arcs $(s,i)$, $i\in N_1$, then there exists a feasible flow given by the $x_{ij}$ values in the arcs $(i,j)\in A$ of the original network.

Residual Network

Many algorithms for max flow employ the concept of residual networks. For each arc $(i,j)\in A$ with capacity $u_{ij}$ and flow $x_{ij}$, we split the arc into a forward arc $(i,j)$ with residual $r_{ij}=u_{ij}-x_{ij}$ and backward arc $(j,i)$ with residual $r_{ji}=x_{ji}$.

The residual capacity, $r_{ij}$, of an arc $(i,j)$ is given by

$$r_{ij}=u_{ij}-x_{ij}+x_{ji}$$

and denotes the maximum additional flow we can send from $i$ to $j$ using arcs $(i,j)$ and $(j,i)$. The residual network $G(x)$ contains all nodes $i\in N$ and all arcs $(i,j)$ with $r_{ij}>0$.

Example:

Consider the network $G$ below where arcs are labeled $x_{ij},u_{ij}$.

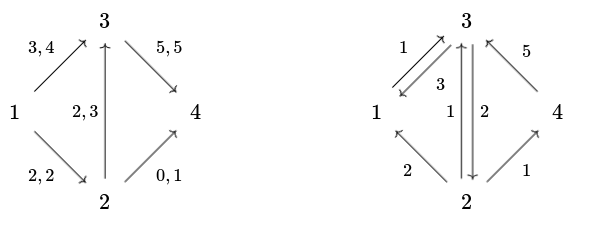
On the left is the original network and on the right is the residual network $G(x)$. Notice that $G(x)$ has an $s-t$ path $P$ given by $1-3-2-4$ which we could push an additional 1 unit of flow along. Such a path is called an augmenting path. The residual capacity of an augmenting path $P$ is

$$\delta (P)=\underset{(i,j)\in P}{\min }\{r_{ij}\}$$

We say to augment along $P$ is to send $\delta (P)$ units along each arc in $P$ and modify $x$ and $G(x)$ accordingly. Thus, if we push $\delta (P)=1$ unit of flow along $P$ in our example, our new network becomes:

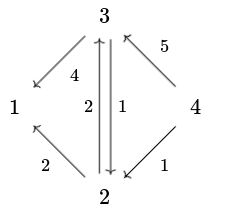
Notice now that there are no $s-t$ paths in $G(x)$. We claim this flow $x$ is optimal.

The Generic Augmenting Path Algorithm

Assume ${\ell }_{ij}=0$ for all $(i,j)\in A$.

Algorithm 5 The Generic Augmenting Path Algorithm

procedure FordFulkerson($G,s,t$)

$x:=0$;

initialize $G(x)$;

while $G(x)$ has a path $P$ from $s$ to $t$ do

augment $\delta(P)$ units of flow along $P$;

updtae $x$ and $G(x)$;

end while

end procedure

Once the algorithm has finished one may obtain the optimal $x_{ij}$ values from the final $G(x)$. Recall that $r_{ij}=u_{ij}-x_{ij}+x_{ji}$, i.e., $x_{ij}-x_{ji}=u_{ij}-r_{ij}$. If $u_{ij}\ge r_{ij}$ we set $x_{ij}=u_{ij}-r_{ij}$ and $x_{ji}=0$. Otherwise, we set $x_{ij}=0$ and $x_{ji}=r_{ij}-u_{ij}$.

This algorithm halts due to the following properties:

1. The residual capacities $r_{ij}$ are integral after each iteration.
2. The capacity of each augmenting path is at least 1.
3. Augmenting along a path $P$ decreases $r_{si}$ for some arc $(s,i)$ by at least one unit.
4. Augmentation never increases $r_{si}$ for any $i$.
5. ${\sigma }_{(s,i)\in A}{r}_{si}$ keeps decreasing and is lower bounded by zero.

One may show that the number of augmentations needed is $O(nU)$ where $U=\max \{u_{ij}\}$.

Max-Flow Min-Cut Theorem

The max-flow min-cut theorem (MFMC) theorem determines when a flow $x$ is optimal.

Def

An $s-t$ cut is a partition of node set $N$ in two disjoint sets $S,\overline{S}$ such that $s\in S$, $t\in \overline{S}$. A forward arc is an arc $(i,j)\in A$ with $i\in S$ and $j\in \overline{S}$. A backward arc is an arc $(i,j)\in A$ with $i\in \overline{S}$ and $j\in S$. The capacity of an $s-t$ cut $[S,\overline{S}]$ is given by

$$u[S,\overline{S}]=\sum _{i\in S,j\in \overline{S},(i,j)\in A}{u}_{ij}.$$

Property: The flow value $v$ of any feasible flow $x$ is at most $u[S,\overline{S}]$ for any $s-t$ cut $[S,\overline{S}]$.

Def

The flow across a cut $[S,\overline{S}]$ is given by

$$F_x[S,\overline{S}]=\sum _{i\in S,j\in \overline{S}}{x}_{ij}-\sum _{i\in S,j\in \overline{S}}{x}_{ji}.$$

Property: If $[S,\overline{S}]$ is an $s-t$ cut, then $F_x[S,\overline{S}]=v$.

Property: $F_x[S,\overline{S}]\le u[S,\overline{S}]$ for any $s-t$ cut $[S,\overline{S}]$.

Optimality Conditions for Max-flow

The following statements are equivalent.

1. A flow $x$ is maximum.
2. There is no augmenting path in $G(x)$.
3. There is an $s-t$ cut $[S,\overline{S}]$ whose capacity is equal to the value of the flow $x$, i.e., $u[S,\overline{S}]=v$.

Max-Flow Min-Cut Theorem

The maximum flow value is equal to the minimum capacity of an $s-t$ cut.