Orientation

Orientation

Let $\sigma$ be a simplex. Two orderings of its vertices are equivalent if they differ by an even permutation. Consequently, the orderings of vertices have two equivalence classes (even and odd). Each equivalence class is an orientation of $\sigma$.

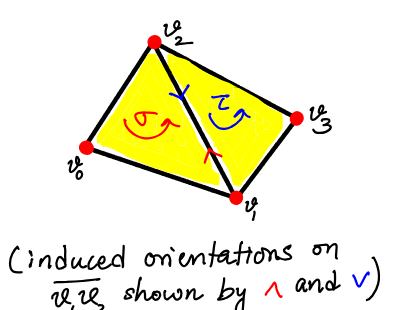
Let $\sigma$ be oriented $[v_0,\dots ,v_k]$. Then this orientation induces an orientation onto it’s faces $\tau =\{v_0,\dots ,\widehat{v_i},\dots ,v_k\}$ given by $[v_0,\dots ,\widehat{v_i},\dots ,v_k]$ if $i$ is even, otherwise it is the opposite orientation.

For example, if $\sigma =[v_0,v_1,v_2]$ then the induced orientations onto its edges are $[v_0,v_1]$, $[v_2,v_0]$ and $[v_1,v_2]$.

Given two $k$-simplices $\sigma$ and $\tau$ that share a common $(k-1)$-face, we say that they are consistently oriented if they induce opposite orientations onto their common $(k-1)$-face.

Orientable

A triangulable $d$-manifold is called orientable if all the $d$-simplices can be consistently oriented.

Orienting a Simplicial Complex

One can orient an orientable $d$-dimensional simplicial complex in two steps:

1. Orient all $d$-simplices based on their signed area.
2. Induce each $d$-simplex’s orientation onto it’s faces.

Note if the complex is not orientable, then this procedure will result in an inconsistent orientation.

Orientation of Triangles

Let $\sigma =[a,b,c]$ be a triangle sitting in ${\mathbb{R}}^3$. Define $e_1=b-a$ and $e_2=c-a$. Then one may find the area of the triangle by finding the magnitude of the cross product,

$$\text{Area}=\frac{1}{2}\Vert e_1\times e_2\Vert .$$

If we want to get the orientation of the triangle, we need to apply the right-hand rule to cross product $e_1\times e_2$. That is, if point your thumb in the direction to $e_1\times e_2$ then your fingers will either curl CCW or CW. This curling gives the orientation of the triangle.

However, the cross product will either give a vector pointed inwards or outwards. One needs to ensure they choose the outward normal vector.

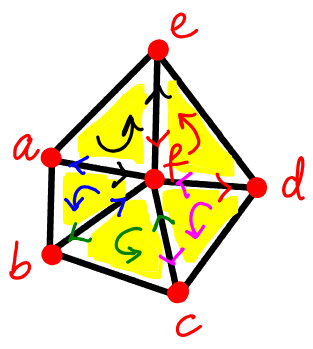
Orientation Propagation

Start by assigning an orientation to a $d$-simplex $\sigma$. We then propagate this orientation to other $d$-simplices $\tau$ that share a $(d-1)$-simplex with $\sigma$.

For example, consider the complex (see below)

$$K=\{\{a,f,e\},\{d,f,e\},\{c,d,f\},\{b,c,f,\},\{a,b,f\}\}.$$

Start with $[a,f,e]$ (CCW orientation). We then look at $\{a,f,e\}$ neighbors ($\{d,e,f\}$ and $\{a,b,f\}$) and orient them so that they’re shared edge ($\{e,f\}$ and $\{a,f\}$) get induced the opposing orientations. Thus, we get $[a,b,f]$ and $[d,e,f]$. Note that $[a,f,e]$ induces $[f,e]$ and $[a,f]$ onto it’s edges, whereas $[a,b,f]$ induces $[f,a]$ and $[d,e,f]$ induces $[e,f]$. We then continue by propagating $[a,b,f]$ and $[d,e,f]$ orientation’s onto their neighbors.