2024-10-08

The non $q$-tame example constructed on 2024-10-07 is not quite right. The following is a better constructed example:

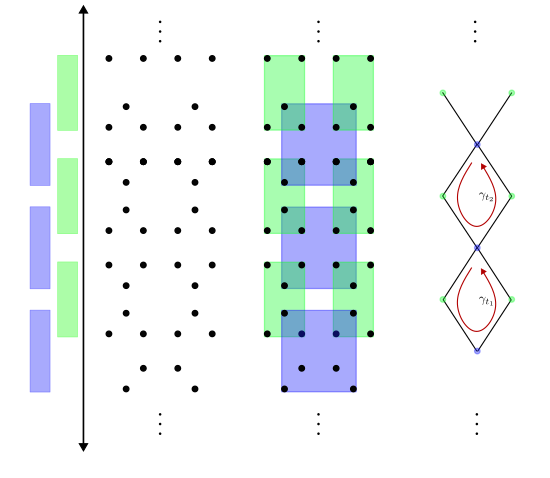
The data points are given by $X={\bigcup }_{i=1}^6{X}_i$ where

$$\begin{array}{rl}{X}_1& =\{(22,75+10k)\mid k\in \mathbb{Z}\}\\ X_2& =\{(24.5,72+15k)\mid k\in \mathbb{Z}\}\cup \{(24.5,68+15k)\mid k\in \mathbb{Z}\}\\ X_3& =\{(27,75+10k)\mid k\in \mathbb{Z}\}\\ X_4& =\{(32,75+10k)\mid k\in \mathbb{Z}\}\\ X_5& =\{(34.5,72+15k)\mid k\in \mathbb{Z}\}\cup \{(34.5,68+15k)\mid k\in \mathbb{Z}\}\\ X_6& =\{(37,75+10k)\mid k\in \mathbb{Z}\}\end{array}$$

We use a filter of $f:X\to \mathbb{R}$ given by $(x,y)\mapsto y$. We cover the real-line with cover elements $\mathcal{U}=\{U_k{\}}_{k\in \mathbb{Z}}\cup \{V_k{\}}_{k\in \mathbb{Z}}$ where

$$\begin{array}{rl}{U}_k& =(64+10k,76+10k)\\ V_k& =(71+15k,88+15k)\end{array}$$

The resulting refined pullback consists of $6\times 11$ boxes $U_k^{\prime }$ and $11\times 12$ boxes $V_k^{\prime }$. Each $U_k^{\prime }$ and $V_k^{\prime }$ overlap to form a $2.5\times 3$ box. So their Steinhaus distance is

$$\begin{array}{rl}{d}_{St}(U_k,V_k)& =1-\frac{\mu (U_k\cap V_k)}{\mu (U_k\cup V_k)}\\ & =1-\frac{6.5}{190.5}\\ & =\frac{368}{381}.\end{array}$$

So in the filtration, all edges are born at time $368/381$. Define the cycle ${\gamma }_k$ that loops around diamond $k$. Then the set $\{{\gamma }_k{\}}_{k\in \mathbb{Z}}$ forms a linearly independent set, i.e., the first homology group has infinite dimension. Therefore, the map between the first homology group at $\alpha =367/381$ and at $\alpha =368/381$ has infinite rank, i.e., it is not $q$-tame.