Types of Network Flow Problems

Notation:

• $G=(N,A)$ a directed network with nodes $N$ and arcs $A\subset N\times N$.
• $|N|=n$
• $|A|=m$
• $c_{ij}$ is the unit cost of arc $(i,j)\in A$. Default value is 0.
• $u_{ij}$ is the capacity of arc $(i,j)\in A$. We always assume that $u_{ij}$ is positive. Default value is $+\infty$.
• ${\ell }_{ij}$ is the lower bound of flow of arc $(i.j)\in A$. We always assume that ${\ell }_{ij}$ is non-negative. Default value is 0.
• $b(i)$ is the supply/demand at a node $i\in N$. Default value is 0.
  • If $b(i)>0$, then it is a supply node.
  • If $b(i)<0$, then it is a demand node.
  • If $b(i)=0$, then it is a transshipment node.

The goal of a network flow problem is to find the flow $x_{ij}$ through every arc $(i,j)\in A$ such that all bounds are satisfied and supply/demand is met at each node $i\in N$ and the total cost is minimum.

We typically assume that the total supply is equal to the total demand, i.e.,

$$\sum _{i\in N}b(i)=0.$$

The min-cost flow problem can be viewed as the following LP:

$$\begin{array}{rlr}& \text{minimize}& \sum _{(i,j)\in A}{c}_{ij}{x}_{ij}\\ & \text{subject to}& \sum _{(i,j)\in A}{x}_{ij}-\sum _{(j,i)\in A}{x}_{ji}=b(i),\forall i\in N\\ & & {\ell }_{ij}\le x_{ij}\le u_{ij},\forall (i,j)\in A\end{array}$$

The first constraint states that at every node $i\in N$, the outflow minus the inflow should equal the supply/demand. The second constraint ensures that the flow through each arc is between our lower bound and upper bounds.

Min-Cost Flow (MCF) Problem

Objective: Determine a least cost shipment of a commodity through a network in order to satisfy demands at certain nodes using supply at certain other nodes.

For example, consider the network

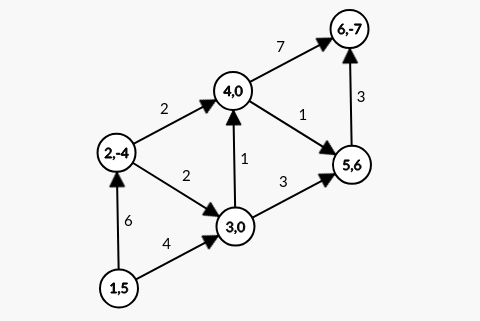
where a node $i$ is denoted $i,b(i)$. We want disperse goods from the supply nodes (1 and 5) to the demand nodes (2 and 6) with the lowest cost. In this example, the only parameters specified are the $b(i)$ and the costs $c_{ij}$. The remaining parameters are assumed to be their default value.

The min-cost flow problem is the most general network flow problem.

Shortest Path Problem

Objective: Find a path of minimum cost from a source (or origin) node $s$ to a terminus (or destination) node $t$ in some network $G=(N,A)$.

For example, in the network

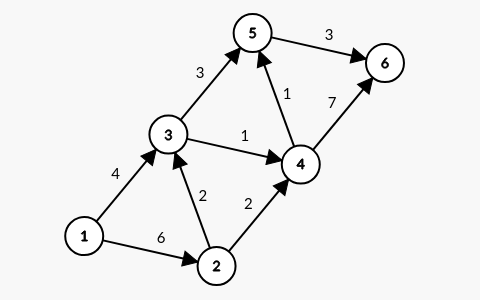
The path of minimum cost from 1 to 6 is $1\to 3\to 4\to 5\to 6$. In the graph above, the only parameters specified are the costs $c_{ij}$.

We can represent the shortest path problem as a min-cost flow problem. We set our source node $s$ to have a supply of 1 and the terminus node $t$ to have a demand of 1. The remaining nodes are transshipment nodes ($b(i)=0$ for all $i\ne s,t$). We set the lower bound ${\ell }_{ij}=0$ for all $(i,j)\in A$. For the upper bounds, we use any positive value. The intuition is that we are sending exactly one unit of flow from $s$ to $t$. Once the MCF problem has been solved, the $x_{ij}$-values that are 1 describe the shortest path.

Maximum Flow Problem

Objective: Find a feasible flow (i.e. a solution that honors the capacity limits on arcs) that sends the maximum amount of flow from a source node $s$ to a terminus node $t$.

For example,

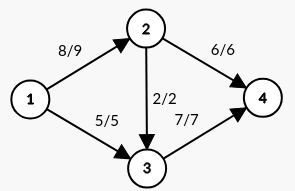
where arcs are labeled by $x_{ij}/u_{ij}$. This is the maximum amount of flow from $s=1$ to $t=4$ for this network because we need that the outflow of $s$ is equal to the inflow of $t$. This is indeed satisfied, since the outflow of 1 is $8+5=13$ and the inflow of 4 is $6+7=13$. If we added an additional unit of flow along the $(1,2)$ arc, then the additional unit of flow would backup at node 2.

Note that nodes 2 and 3 have total inflow equal to total outflow. Hence, they are transshipment nodes.

The only parameters specified here are the arc capacities $u_{ij}$. All other parameters are their default values.

We can represent a max flow problem as a min-cost flow problem. We add an additional arc from the terminus $t$ to the source $s$ with a cost of -1 and a capacity of $+\infty$. All original arcs are given the default cost of 0.

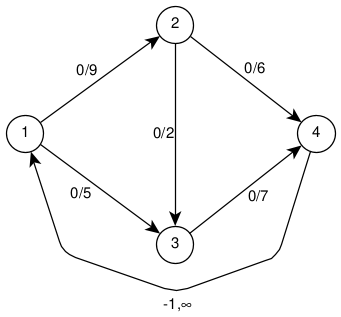
Here the the arcs $(i,j)$ are labeled by $c_{ij}/u_{ij}$. Since $c_{41}<0$ and we are trying to minimize cost, the MCF will send as much flow as possible through arc $(t,s)$. The total amount sent is capped due to the capacities $u_{ij}$ of the original network.

This example is also a min-cost circulation problem - there are no supply/demand nodes and the flow circulates through the network.

Transportation Problem

A special case of the MCF is the transportation problem, which occurs when the network is a bipartite graph, i.e.,

$$N=N_1\cup N_2$$

where $N_1$ is a set of supply nodes and $N_2$ is a set of demand nodes and each $(i,j)\in A$ has $i\in N_1$ and $j\in N_2$. We can intuitively think of it as sending goods from a set of warehouses to various stores to be sold.

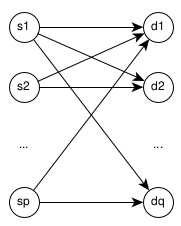
A transportation problem is called balanced if

$$\sum _{s_i\in N_1}b(s_i)=-\sum _{d_j\in N_2}b(d_j).$$

Assignment Problem

Objective: Given $p$ people and $p$ jobs and cost $c_{ij}$ for assigning person $i$ to job $j$. The goal is to assign each person to a job so that the total cost is minimized.

This is a special case of the transportation problem where $|N_1|=|N_2|$, $b(i)=1$ for each $i\in N_1$ and $b(j)=-1$ for each $j\in N_2$.