Basic Optimization

The most basic optimization problem is

$$\begin{array}{rlrl}& \underset{x}{\mathrm{minimize}}& & f(x)\\ & \text{subject to}& & x\in \mathcal{X}.\end{array}$$

We call $x$ a design point. Design points can be represented as a vector of values. The function $f$ is called the objective function. The set $\mathcal{X}$ is called the feasible set. The goal is to find the $x\in \mathcal{X}$ that minimizes the objective function. We call such $x$ a solution or minimizer. Often optimization problems have constraints which provides limitations to the feasible set. For example,

$$\begin{array}{rlrl}& \underset{x_1,x_2}{\mathrm{minimize}}& & f(x_1,x_2)\\ & \text{subject to}& & x_1\ge 0\\ & & & x_2\ge 0\\ & & & x_1+x_2\le 1\end{array}$$

has the feasible set shown in the figure below. 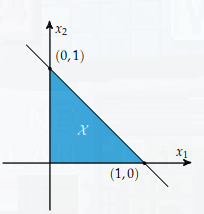One simple approach to optimization of a function is to look at the set of critical points that lie inside the feasible set. Unfortunately, it is not always easy to tell if a critical point is a global minimum; typically we can only check if it is a local minimum, i.e., there is some $\delta >0$ such that $f(x^{\ast })\le f(x)$ for all $x$ such that $\Vert x-x^{\ast }\Vert <\delta$.

Local minima fall into two categories: strong and weak. A strong local minima, also known as a strict local minima, is a point $x^{\ast }$ such that for some $\delta >0$ it follows that $f(x^{\ast })<f(x)$ whenever $x^{\ast }\ne x$ and $\Vert x^{\ast }-x\Vert <\delta$.

Note that while a derivative of zero is a necessary condition for a local minima, it is not sufficient as the point may be an inflection point.

Univariate

A necessary condition for a design point $x$ to be a local minimum is that

1. $f^{\prime }(x^{\ast })=0$, the first-order necessary condition (FONC)
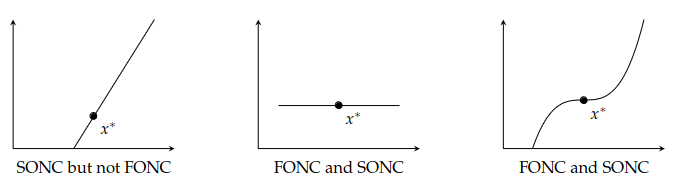
2. $f^{\prime \prime }(x^{\ast })\ge 0$, the second-order necessary condition (SONC). For local maximum we simply SONC to $f^{\prime \prime }(x^{\ast })\le 0$. While these conditions are necessary, they are not sufficient. This can be seen in the three functions below: These conditions can be derived via Taylor expansion. Let $x^{\ast }$ be a local minimum. Notice that

$$\begin{array}{rl}f(x^{\ast }+h)& =f(x^{\ast })+h{f}^{\prime }(x^{\ast })+O(h^2)\\ f(x^{\ast }-h)& =f(x^{\ast })-h{f}^{\prime }(x^{\ast })+O(h^2)\end{array}$$

If $x^{\ast }$ is a local minimum, then

$$f(x^{\ast }+h)\ge f(x^{\ast })\text{ and }f(x^{\ast }-h)\ge f(x^{\ast }).$$

Therefore, combining these two gives us that

$$h{f}^{\prime }(x^{\ast })\ge 0\text{ and }h{f}^{\prime }(x^{\ast })\le 0\Rightarrow f^{\prime }(x^{\ast })=0.$$

As for the second-order necessary condition, notice that

$$f(x^{\ast }+h)=f(x^{\ast })+h{f}^{\prime }(x^{\ast })+\frac{h^2}{2}{f}^{\prime \prime }(x^{\ast })+O(h^3).$$

By the first-order condition,

$$f(x^{\ast }+h)\ge f(x^{\ast })\Rightarrow \frac{h^2}{2}{f}^{\prime \prime }(x^{\ast })\ge 0\Rightarrow f^{\prime \prime }(x^{\ast })\ge 0.$$

Multivariate

We get similar necessary conditions for $x$ to be a local minimum of a multivariate function:

1. $\nabla f(x)=0$, the first-order necessary condition (FONC)
2. $x^{\top }{\nabla }^{2}fx\ge 0$ for all $x$, the second-order necessary condition (SONC).

Recall that for scalar-valued differentiable function $f:{\mathbb{R}}^n\to \mathbb{R}$, the gradient is the vector field

$$\nabla f(x)=⟨\text{dv}f{x}_1(p),\cdots ,\text{dv}f{x}_n(x)⟩.$$

Given a function $f:{\mathbb{R}}^n\to \mathbb{R}$, the Hessian matrix ${\nabla }^{2}f$ is is the $n\times n$ matrix of second-order partial derivatives

$${\nabla }^{2}f=\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}& \frac{{\partial }^{2}f}{\partial x_1{x}_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_1{x}_n}\\ \frac{{\partial }^{2}f}{\partial x_2{x}_1}& \frac{{\partial }^{2}f}{\partial x_2^2}& \cdots & \frac{{\partial }^{2}f}{\partial x_2{x}_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f}{\partial x_n{z}_1}& \frac{{\partial }^{2}f}{\partial x_n{x}_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_n^2}.\end{array}\right].$$

Thus, the SONC is checking when the Hessian matrix is positive semi-definite.

Some example cases are given in the figure below.