Simplices

Let $S=\{p_0,\dots ,p_k\}\subset {\mathbb{R}}^d$. Recall that a linear combination of $S$ is a sum of the form

$$x=\sum _{i=0}^k{\lambda }_i{p}_i$$

where ${\lambda }_1,\dots ,{\lambda }_k\in \mathbb{R}$. If ${\sum }_{i=0}^k{\lambda }_i=1$, then $x$ is an affine combination of $S$. If in addition, each ${\lambda }_i\ge 0$, then $x$ is a convex combination of $S$.

Convex Hull

The set of all convex combinations of a set $S=\{p_0,\dots ,p_k\}\subset {\mathbb{R}}^d$ is called the convex hull of $S$, i.e.,

$$\text{conv}(S)=\left\{\sum _{i=1}^k{\lambda }_i{p}_i:{\lambda }_i\ge 0,\forall i,\sum _{i=1}^k{\lambda }_i=1\right\}$$

We say that a set $S=\{p_0,\dots ,p_k\}\subseteq {\mathbb{R}}^d$ is affinely independent if no $p_i\in S$ is the affine combination of other points in $S$. In the case that $|S|=1$, we say the singleton set $\{p_0\}$ is affinely independent even if $p_0=0$.

Simplices are simply the convex hull of affinely independent sets.

Simplex

The convex hull of affinely independent points $S=\{v_0,\dots ,v_k\}$ is called a $k$-simplex.

Notice that the dimension of a simplex with $k+1$ vertices is $k$.

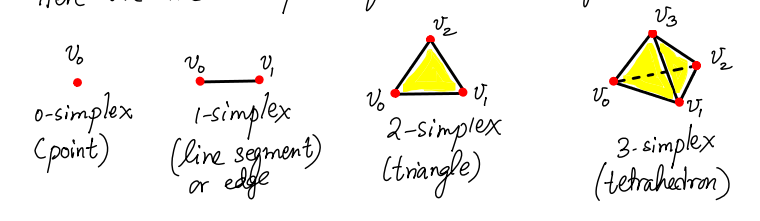
A $k$-simplex is composed of lower dimensional simplices. For example, the 2-simplex $\Delta v_0{v}_1{v}_2$ contains the vertices $v_0,v_1,v_2$ and edges $\overline{v_0{v}_1}$, $\overline{v_0{v}_2}$, $\overline{v_1{v}_2}$.

Face

Let $\sigma$ be the $k$-simplex defined on $S=\{v_0,\dots ,v_k\}$. Then any simplex $\tau$ defined on a nonempty subset $T$ of $S$ is a face of $\sigma$, and $\sigma$ is a coface of $\tau$. We denote faces by $\tau \le \sigma$ or $\tau ⪯\sigma$.

Note the lack of dimensionality in our definition. Hence, we consider the vertex $v_0$ to be a face of $\Delta v_0{v}_1{v}_2$.

Simplicial Complex

We can stitch several simplices together to form a larger object called a simplicial complex.

Simplicial Complex

A simplicial complex $K$ is a set of simplices such that

1. if $\sigma \in K$ and $\tau \le \sigma$, then $\tau \in K$; and
2. if $\sigma ,{\sigma }^{\prime }\in K$ such that $\sigma \cap {\sigma }^{\prime }\ne \varnothing$, then $\sigma \cap {\sigma }^{\prime }\le \sigma ,{\sigma }^{\prime }$.

In words, the first condition states that all faces of simplices must be in the complex. Where as the second states that the non-empty intersection of two simplices is a face of both simplices.

Note that the definition has no criterion on the cardinality of $K$. However, we focus on finite simplicial complexes.

We define the dimension of a simplicial complex $K$ to be the highest dimensional simplex, i.e.,

$$\dim K=\max \{\dim \sigma :\sigma \in K\}.$$

A simplicial complex $K$ is a collection of simplices lying in some ambient Euclidean space. If we take the union of each simplex, we get the underlying space:

$$|K|=\bigcup _{\sigma \in K}\sigma .$$

Sometimes $|K|$ is called the polyhedron or polytope of $K$.

Abstract Simplicial Complexes

Computationally, we cannot store every point lying in a simplex. Instead it is common to store a list of vertices, then represent simplices by a set of indices pointing to vertices. For example, if a $k$-simplex had vertices $v_0,\dots ,v_k$, then we would store the set $\{0,\dots ,k\}$ instead.

This forms an abstract simplicial complex, which is simply a set-theoretic extension of simplicial complexes:

Abstract Simplicial Complex

An abstract simplicial complex (ASC) is a collection $\mathcal{S}$ of finite non-empty sets such that $A\in \mathcal{S}$ and $B$ is a non-empty subset of $A$, then $B\in \mathcal{S}$.

Typically, we require that the elements of $\mathcal{S}$ to be finite sets. That way, we can still call elements $A\in \mathcal{S}$ simplices and refer to their dimension by $|A|-1$. Then it is the same definition as before for the dimension of $\mathcal{S}$:

$$\dim \mathcal{S}=\max \{|A|-1:A\in \mathcal{S}\}.$$

Given any simplicial complex $K$, we can construct an ASC by just taking the vertices. Such a constrution is called the vertex scheme of $K$.

It is worthwhile to note that any abstract simplicial complex $\mathcal{S}$ has a geometric realization $K$:

Geometric Realization

Every abstract simplicial complex $\mathcal{S}$ with $\dim \mathcal{S}=d$ has a geometric realization in ${\mathbb{R}}^{2d+1}$.

Note that often ASCs can be realized in lower dimensions, however, we can always guarantee realize by working in ${\mathbb{R}}^{2d+1}$. The general idea of a construction is to map the vertices of $\mathcal{S}$ (the singleton sets) injectively to points in ${\mathbb{R}}^{2d+1}$ such that they are in general position, that is, there is no hyperplane containing more than $d$ points. As a result, the vertices will be affinely independent.

Comparing Abstract Simplicial Complexes

Isomorphic

Two ASCs ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$ are said to be isomorphic, denoted ${\mathcal{S}}_1\approx {\mathcal{S}}_2$, if there is a bijection $\phi :\text{Vert}({\mathcal{S}}_1)\to \text{Vert}({\mathcal{S}}_2)$ between the vertex sets such that $A\in {\mathcal{S}}_1$ if and only if $\phi (A)\in {\mathcal{S}}_2$.

In other words, every simplex in ${\mathcal{S}}_1$ corresponds uniquely to a simplex in ${\mathcal{S}}_2$.

The vertex scheme of simplicial complexes turn out to be useful tools to compare simplicial complexes.

Thm

Two simplicial complexes $K_1$ and $K_2$ are simpliicially homeomorphic (denoted $K_1\cong K_2$) if and only if their vertex schemes ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$ are isomorphic.

Some sources say $K_1$ and $K_2$ are isomorphic instead.

One may easily see that if $K_1\cong K_2$, then their underlying spaces $|K_1|$ and $|K_2|$ are homeomorphic. However, the converse does not hold in general. For example with

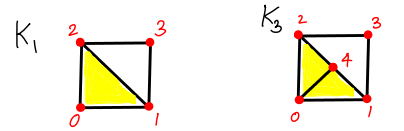
we get that $K_1\ncong K_3$ due to the additional vertex, but $|K_1|\approx |K_3|$.