k-nearest Neighbors

The k-nearest neighbors algorithm (k-NN) is a non-parametric supervised learning method for classification and regression. In k-NN classification an object is assigned to the class most common among its $k$ nearest neighbors. The algorithm relies on a metric for classification. If data has varying scales or units then normalizing the training data can improve its accuracy.

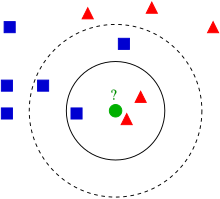
In the example above, if we use $k=3$ (three nearest neighbors) then the green circle will be classified with the triangles since there are more triangles than squares. However, if we use $k=5$, then there are three neighboring squares and 2 neighboring triangles resulting in an assignment of square.

The choice of number of neighbors, $k$, depends heavily on the data. In general, a larger $k$ suppresses the effects of noise but makes the classification boundaries less distinct.

The data should come in the form $(X_1,Y_1),\dots ,(X_n,Y_n)\in {\mathbb{R}}^d\times \{1,2\}$, where $Y$ is the class label of $X$. We also require a norm $\Vert \cdot \Vert$ on ${\mathbb{R}}^d$. A common choice for continuous variables is Euclidean distance. For discrete variables a common choice is Hamming distance.

Skewed data can result in the more frequent class dominating the prediction of a new example. A way to overcome this problem is to weight the classification by taking into account the distance from the test point to each of its $k$-nearest neighbors.