Homotopy

Homotopy

Let $f,g:X\to Y$ be continuous maps from topological spaces $X$ and $Y$. A homotopy between $f$ and $g$ is a continuous map $H:X\times [0,1]\to Y$ such that $H(x,0)=f(x)\text{ and }H(x,1)=g(x)$ for all $x\in X$. We then say $f$ is homotopy equivalent to $g$ or that $f$ is homotopic to $g$ and denote this equivalence relation by $f\simeq g$.

You can think of $H$ as a time-series of functions $f_t(x):X\to Y$ given by $f_t(x)=H(x,t)$ such that $f_0=f$ and $f_1=g$. The idea is that we can continuously transition between the two maps $f$ and $g$.

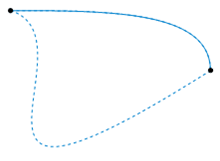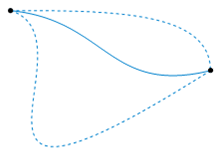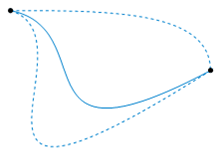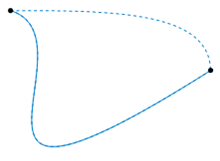
As an example, let $f,g:\mathbb{R}\to {\mathbb{R}}^2$ be given by $f(x)=(x,x^3)$ and $g(x)=(x,e^x)$. Then the map $H:\mathbb{R}\times [0,1]\to {\mathbb{R}}^2$ given by

$$H(x,t)=(x,(1-t)x^3+t{e}^x)$$

is a homotopy between $f$ and $g$. This example also highlights a simple construction of homotopy maps, that is, a straight-line:

$$H(x,t)=tf(x)+(1-t)g(x).$$

However, not every pair of maps $f$ and $g$ are homotopic as $H$ here may not be well-defined. If we take $f={\text{id}}_{S^1}$ and $g(x)=p$ where $p$ is an arbitrary point $p\in S^1$, then $f\not\simeq g$. If we took our “straight-line homotopy”, then $H(x,\frac{1}{2})=\frac{1}{2}x+\frac{1}{2}p$ gives the midpoint between $x$ and $p$, which clearly does not lie in $S^1$.

One special case of homotopy is retractions.

Deformation Retract

A subset $Y\subseteq X$ is a retract of $X$ if there is a continuous map $r:X\to Y$ called a retraction such that $r(y)=y$ for all $y\in Y$. If $r$ is homotopy equivalent to ${\text{id}}_X$, then $Y$ is a deformation retract and $r$ is a deformation retraction.

For example, consider the set $X$ below. Then $Y_1$ is a deformation retract of $X$. We can continue to deformation retract to get the skeleton $Y_2$.

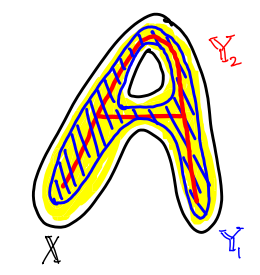
As a result, $X$, $Y_1$ and $Y_2$ are homotopy equivalent.

Another example is the $n$-sphere $S^n$ is a deformation retract of ${\mathbb{R}}^{n+1}\backslash \{0\}$. This can be seen by the map

$$H(x,t)=(1-t)x+t\frac{x}{\Vert x\Vert }.$$

Notice that at $t=0$ we get the identity map $H(x,0)=x$ and at $t=1$ we get $H(x,1)=x/\Vert x\Vert$ which when restricted to $S^n$ is the identity map.

Homotopy Equivalent

We say two spaces $X$ and $Y$ are homotopy equivalent or have the same homotopy type, if there are continuous maps $f:X\to Y$ and $g:Y\to X$ such that $f\circ g\simeq {\text{id}}_Y$ and $g\circ f\simeq {\text{id}}_X$. We denote this relationship by $X\simeq Y$.

The $n$-sphere $S^n$ is homotopy equivalent to ${\mathbb{R}}^{n+1}\setminus \{0\}$. This can be seen by the deformation retract given above. In fact, all deformation retracts are homotopy equivalences.

Moreover, if two spaces are homeomorphic, they have the same homotopy type. Indeed, let $f:X\to Y$ be a homeomorphism. Then $f\circ f^{-1}$ is clearly homotopic to ${\text{id}}_Y$ (in fact they are equal). Likewise, $f^{-1}\circ f$ is homotopic (again, actually equal) to ${\text{id}}_X$.

However, the converse is not true. For example, in our deformation retract from $X$ to $Y_2$ in the “fat A” example, we get that $X$ and $Y_2$ are homotopy equivalent. But, they are not homeomorphic since $X$ is a 2-manifold with boundary and $Y_2$ is a 1-manifold with boundary.

Another common examples is that ${\mathbb{R}}^n$ is homotopy equivalent to a single point $p$. This can be seen by the map

$$H(x,t)=tp+(1-t)x.$$

At $t=0$ we get ${\text{id}}_{{\mathbb{R}}^n}$ and at $t=1$ we get ${\text{id}}_{\{p\}}$. This is a special case of homotopy equivalence.

Contractible

If $X$ is a homotopy equivalent to a single point, then $X$ is contractible.