Delaunay

A common question is how to construct a simplicial complex given a data set. One such method is known as Delaunay complex. We seek to build up the Delaunay complex construction.

Nerve

Let $F$ be a finite collection of sets in ${\mathbb{R}}^d$. The nerve of $F$ is all sub-collections of $F$ with nonempty intersection, i.e.,

$$\text{Nrv}F=\{X\subseteq F:\bigcap _{S\in X}S\ne \varnothing \}.$$

Notice that the nerve forms an abstract simplicial complex. Indeed, if $Y$ is a non-empty subset of $X\in \text{Nrv}F$, then ${\bigcap }_{S\in Y}S\supseteq {\bigcap }_{S\in X}S\ne \varnothing$.

As an example, consider the collection of sets $F$ below composed of the black set $B$, blue set $L$, red set $R$ and pink set $P$.

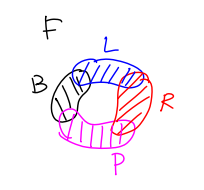
The nerve would then be all sub-collections of $k$ sets for $k=1,2,3,4$ whose intersection is non-empty. Thus, we get that

$$\text{Nrv}F=\{\{B\},\{L\},\{R\},\{P\},\{B,L\},\{L,R\},\{R.P\},\{B,P\}\}.$$

So we get that $\dim \text{Nrv}F=1$.

Voronoi Diagram

Voronoi cell

Let $S=\{v_0,\dots ,v_n\}$ be a finite set of points in ${\mathbb{R}}^d$. The Voronoi cell of $v_j\in S$ is the set of points closest to $v_j$, i.e.,

$$V_{v_j}=\{x\in {\mathbb{R}}^d:\Vert x-v_j\Vert \le \Vert x-v_i\Vert ,\forall v_i\in S\}.$$

In the case that $S=\{v_0,v_1\}$, the Voronoi cells $V_{v_0}$ and $V_{v_1}$ are the half-planes divided by the perpendicular bisector equidistant from the points. As we introduce more points, we repeatedly take the perpendicular bisectors. As a result, cells $V_{v_i}$ become the intersection of a set of half-spaces forming a convex polyhedron.

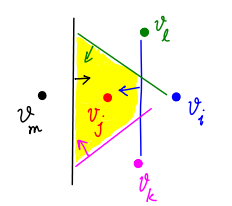
Voronoi Diagram

The collection of Voronoi cells $V_{v_1},\dots ,V_{v_n}$ is called the Voronoi diagram.

Delaunay Complex

The Delaunay complex is defined to be the nerve of the Voronoi diagram.

Delaunay Complex

The Delaunay complex of a set $S=\{v_0,\dots ,v_n\}\subset {\mathbb{R}}^d$ is given as

$${\text{Del}}_S=\left\{\sigma \subseteq S:\bigcap _{v_j\in \sigma }{V}_{v_j}\ne \varnothing \right\}.$$

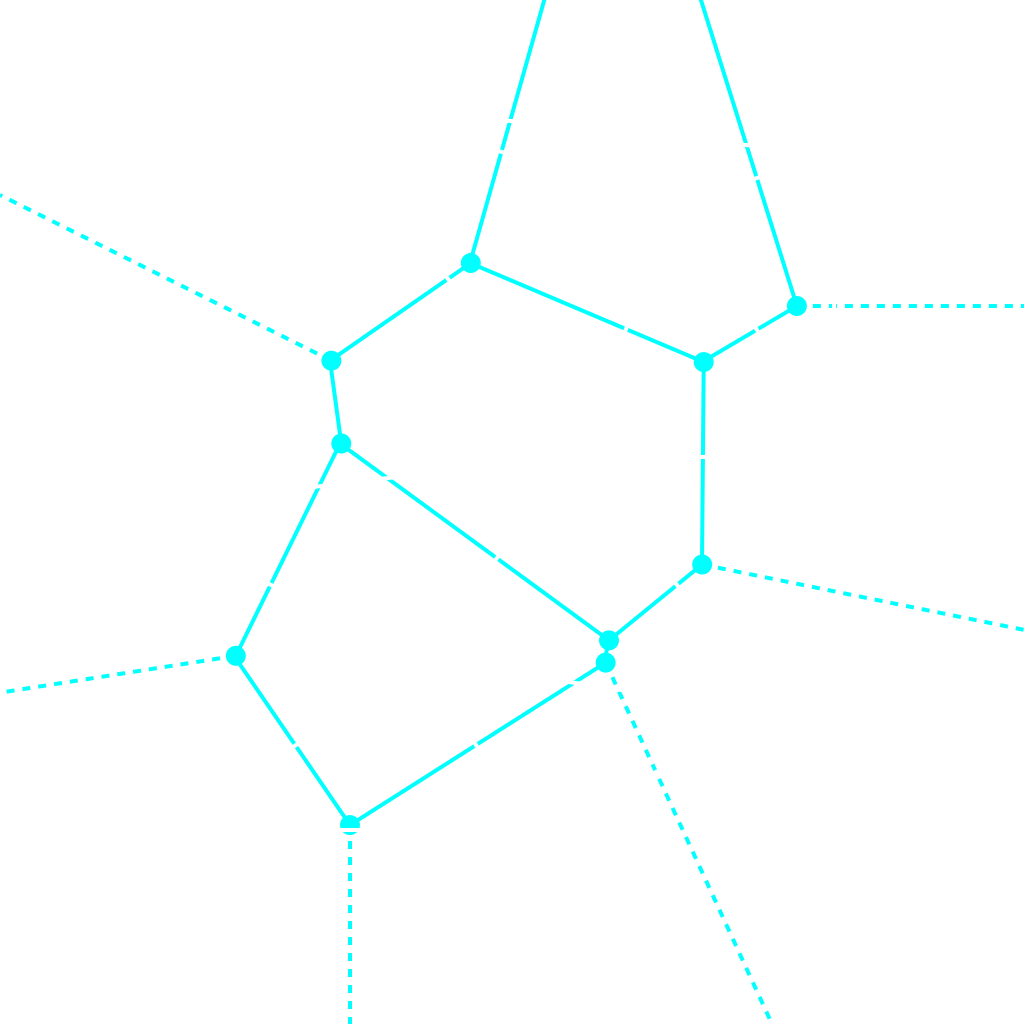
For example, consider the Delaunay complex shown below in wireframe (white). Notice that each vertex corresponds to a single Voronoi cell (cyan). The dashed lines indicate they go on infinitely.

It is worth noting that not all Delaunay complexes in ${\mathbb{R}}^2$ are composed of triangles. If we take our set $S$ to be four points along the unit circle, we get the four Voronoi cells intersect at the origin:

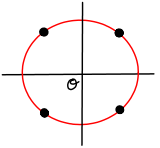
In other words,when we take the nerve we get the tetrahedron $\{V_{v_1},V_{v_2},V_{v_3},V_{v_4}\}$. However, by shifting one vertex by some small $ϵ$, we no longer get a four-way intersection.

General Position

A set of point $S\subset {\mathbb{R}}^d$ is in general position if no $d+2$ points in $S$ lie on a common $(d-1)$-sphere.

For example, in the tetrahedron example (where $d=2$), we had four points of $S$ lying on the unit circle ($1$-sphere).

When the points are in general position, then there is no $(d+2)$ Voronoi cells with a common intersection. Hence, if $\sigma \in {\text{Del}}_S$, then $\dim \sigma \le d$.

Bower-Watson Algorithm

The Bower-Watson algorithm is an incremental algorithm for constructing the Delaunay triangulation of a finite set of points. It has a time complexity of $O(n^2)$, however, this can be optimized down to $O(n\log n)$.

The algorithm starts by constructing a triangle large enough to contain all points of $S$.

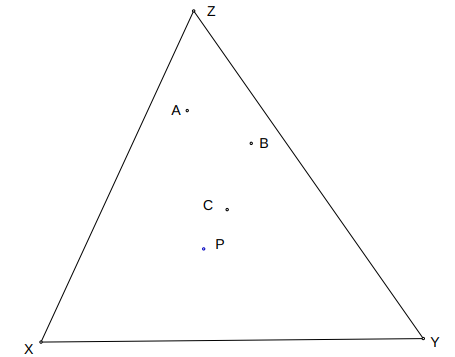
It then adds points one at a time. For each point $P$ added, it searches each triangle checking if $P$ lies inside the triangles circumcircle. If so, it marks the triangle as a bad triangle needing to be removed. For example, below we see that $P$ is inside the circumcircle of triangle $\Delta ACX$, so we mark it for removal.

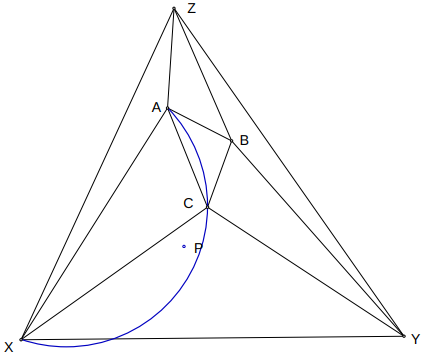
Once we’ve removed all bad triangles, we replace them with new triangles that contain the new point $P$. So our bad triangle $\Delta ACX$ is replaced with triangles $\Delta ACP$ and $\Delta XPY$.

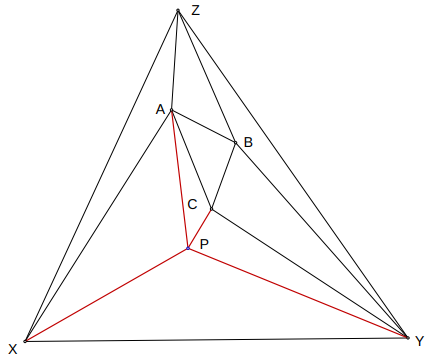
Once we’ve added every point, we remove all triangles that have an edge of the original triangle.

The full algorithm:

1. Choose a triangle ST containing the set of points P in its interior and initialize D = {ST}.
2. For each p in P:
	Initialize a list of edges E marked for deletion
	For each T in D:
		If p is in the circumcircle of T
			Delete T from D
			Add each edge of T to E
	Delete the edges from E that belong to two different deleted triangles
	The remaining edges in E form the boundary of the enclosing polygon.
	Add the triangles that are formed by joining p to each of the vertices of     edges in E to D.
3. Delete any triangles from D that share a vertex with ST
4. The remaining triangles are the Delaunay triangles.

Note the Bower-Watson algorithm can be applied to higher dimensions. Simply replace triangles with $d$-simplices and circumcircle with $(d-1)$-circumsphere.