Derivatives and Gradients

Derivatives

The derivatives $f^{\prime }(x)$ of a univariate function $f:\mathbb{R}\to \mathbb{R}$ is the rate at which the value of $f$ changes at $x$. It is often visualized as the tangent line to the graph at $x$. The derivative is a useful tool for providing a linear approximation of the function by stepping along the tangent line:

$$f(x+\Delta x)\approx f(x)+f^{\prime }(x)\Delta x.$$

The limit equation of the derivative has three variants.

• Forward difference:

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

• Central difference:

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h/2)-f(x-h/2)}{h}$$

• Backward difference:

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x)-f(x-h)}{h}$$

Derivatives in Multiple Dimensions

The gradient is a generalization of the derivative to multivariate functions. The gradient of $f:{\mathbb{R}}^n\to \mathbb{R}$ at $x$, denoted $\nabla f(x)$ is the vector

$$\nabla f(x)=⟨\frac{\partial f(x)}{\partial x_1},\cdots ,\frac{\partial f(x)}{\partial x_n}⟩$$

that points in the direction of steepest ascent of the tangent hyperplane.

The Hessian of a multivariate function is the matrix containing all the second-order partial derivatives.

$${\nabla }^{2}f=\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}& \frac{{\partial }^{2}f}{\partial x_1{x}_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_1{x}_n}\\ \frac{{\partial }^{2}f}{\partial x_2{x}_1}& \frac{{\partial }^{2}f}{\partial x_2^2}& \cdots & \frac{{\partial }^{2}f}{\partial x_2{x}_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f}{\partial x_n{z}_1}& \frac{{\partial }^{2}f}{\partial x_n{x}_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_n^2}.\end{array}\right].$$

The directional derivative ${\nabla }_{v}f(x)$ measures the rate of change in a particular direction $s$ at a point $x$. It is defined by a vector variation of the difference quotient.

$${\nabla }_{v}f(\text{x})=\underset{h\to 0}{\lim }\frac{f(\text{x}+h\text{v})-f(\text{x})}{h}.$$

It can be computed by taking the dot product with the gradient,

$${\nabla }_{v}f(x)=\nabla f(x)\cdot v.$$

The directional derivative is maximal in the direction of the gradient and minimal in the direct opposite direction of the gradient.

Numerical Differentiation

Numerically we often approximate the derivative of a function. One such method is finite difference methods where we simply evaluate the difference quotient for small $h$, i.e.,

$$f^{\prime }(x)\approx \frac{f(x+h)-f(x)}{h}.$$

The smaller $h$ is the better the approximation gets. We can find the error term by looking at the Taylor expansion of $f$ about $x$:

$$f(x+h)=f(x)+\frac{f^{\prime }(x)}{1!}h+\frac{f^{\prime \prime }(x)}{2!}{h}^2+\frac{f^{\prime \prime \prime }(x)}{3!}{h}^3+\cdots$$

Solving for $f^{\prime }(x)$ gives us

$$f^{\prime }(x)=\frac{f(x+h)-f(x)}{h}-\frac{f^{\prime \prime }(x)}{2!}h-\frac{f^{\prime \prime \prime }(x)}{3!}{h}^2-\cdots$$

Thus, the forward difference approximates the true derivative with an error term that is $O(h)$. One may show that the central difference method is slightly better with an error term of $O(h^2)$.

Complex Step Method

Finite difference methods run into the issue of choosing a suitable $h$-value. Too small results in floating point errors and too large results in poor approximations. In complex step method we evaluate after taking a step in the imaginary direction:

$$f(x+ih)=f(x)+ih{f}^{\prime }(x)-h^2\frac{f^{\prime \prime }(x)}{2!}-i{h}^3\frac{f^{\prime \prime \prime }(x)}{3!}+\cdots$$

If we take the imaginary component and solve for $f^{\prime }(x)$ we get that

$$f^{\prime }(x)=\frac{\text{Im}(f(x+ih))}{h}+O(h^2).$$

If we instead took the real part we can approximate $f(x)$:

$$f(x)=\text{Re}(f(x+ih))+O(h^2).$$

Hence, with a single evaluation we can approximate both $f(x)$ and $f^{\prime }(x)$.

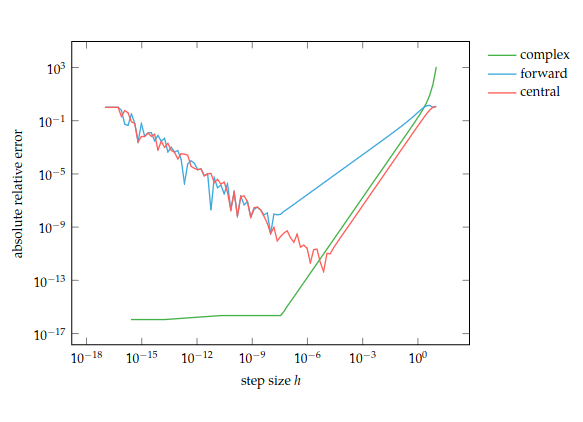
Below is a chart comparing the absolute relative error of complex step, forward difference, and central difference for $\sin (x)$ At $x=1/2$ for various step sizes $h$:

Automatic Differentiation

Imagine taking the partial derivative of the function $f(a,b)=\ln (ab+\max (a,2))$ wit h respect to $a$. Doing so requires applying the chain rule several times. We can automate the process with a computational graph which represents a function with a graph where nodes are operations and edges are input-output relations.

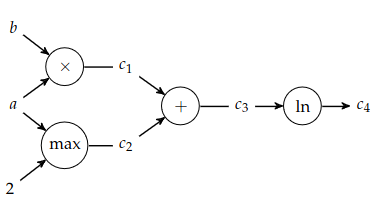
There are two methods for automatically differentiating a function $f$ using its computational graph, forward accumulation and reverse accumulation.

Forward Accumulation

To demonstrate forward accumulation consider $f(a,b)=\ln (ab+\max (a,2))$ at $a=3$, $b=2$.

We start at the computational graph’s source nodes consisting of function inputs and constant values. For each node we find both the value and the partial derivative.

Next, we proceed down the tree one node at a time. We compute the value and local partial derivative using the previous nodes’ values and partial derivatives.

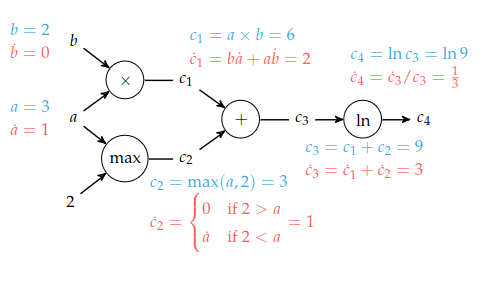
When we are done, we get both $f(3,2)=\ln 9$ and $\partial f/\partial a=1/3$.

It is often beneficial to express the value and partial derivative as a dual number. A dual number is, like complex numbers, written in the form $a+bϵ$ where $a,b\in \mathbb{R}$ and ${ϵ}^2=0$ by definition. We can add and multiply dual numbers:

$$\begin{array}{rl}(a+bϵ)+(c+dϵ)& =(a+c)+(b+d)ϵ\\ (a+bϵ)(c+dϵ)& =(ac)+(ad+bc)ϵ.\end{array}$$

Let $f$ be a smooth function. Notice that if we use the Taylor series,

$$\begin{array}{rl}f(a+bϵ)& =\sum _{k=0}^{\infty }\frac{f^{(k)}(a)}{k!}(a+bϵ-a{)}^k\\ & =\sum _{k=0}^{\infty }\frac{f^{(k)}(a)b^k{ϵ}^k}{k!}\\ & =f(a)+b{f}^{\prime }(a)ϵ+{ϵ}^2\sum _{k=2}^{\infty }\frac{f^{(k)}(a)b^k}{k!}{ϵ}^{k-2}\\ & =f(a)+b{f}^{\prime }(a)ϵ.\end{array}$$

Encoding the function value and partial derivative.

Exercises

Exercise 2.1. Adopt the forward difference method to approximate the Hessian of $f(\text{x})$ using its gradient, $\nabla f(\text{x})$. Answer: Recall that the $i$-th column of ${\nabla }^{2}f$ is given by

$${\left[\frac{{\partial }^{2}f}{\partial x_1\partial x_i},\cdots ,\frac{{\partial }^{2}f}{\partial x_n\partial x_i}\right]}^{\top }$$

We can approximate this vector by using forward difference method on $\nabla f(\text{x})$:

$$\frac{\nabla f(\text{x}+h{e}_i)-\nabla f(\text{x})}{h}$$

where $e_i$ is the the vector with a 1 in the $i$-th position and zeroes elsewhere.

Exercise 2.5. Draw the computational graph for $f(x,y)=\sin (x+y^2)$. Use the computational graph with forward accumulation to compute $\partial f/\partial y$ at $(x,y)=(1,1)$. Label the intermediate values and partial derivatives as they are propagated through the graph. Answer:

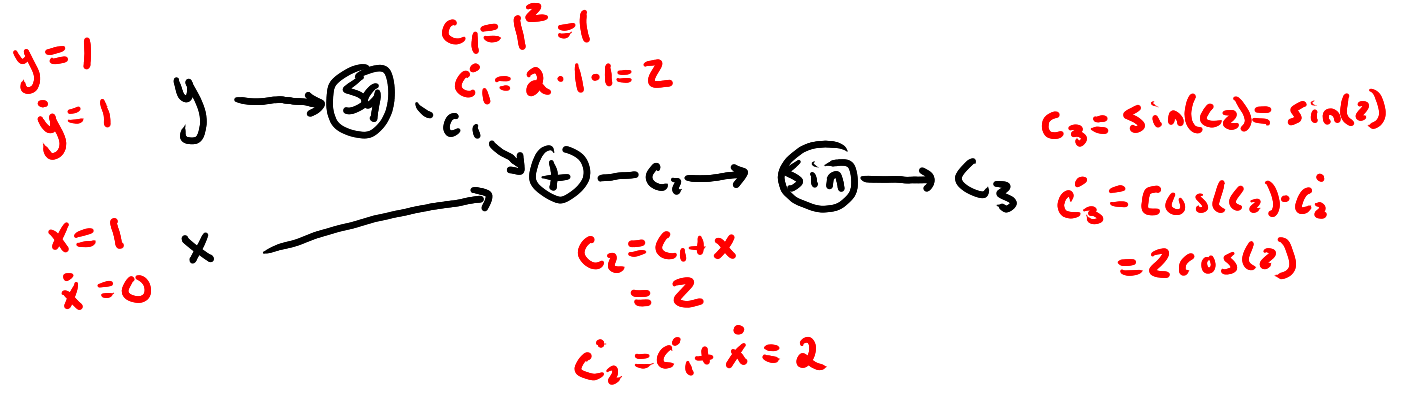We get that $f(1,1)=\sin (2)$ and $\partial f/\partial y{|}_{(1,1)}=2\cos (2)$.

Exercise 2.6. Combine the forward and backward difference methods to obtain a difference method for estimating the second-order derivative of a function $f$ at $x$ using three function evaluations. Answer:

$$\begin{array}{rl}{f}^{\prime \prime }(x)& \approx \frac{f^{\prime }(x+h)-f^{\prime }(x)}{h}\\ & \approx \frac{\frac{f(x+h)-f(x)}{h}-\frac{f(x)-f(x-h)}{h}}{h}\\ & =\frac{f(x+h)-2f(x)+f(x-h)}{h^2}.\end{array}$$