1. Smooth Functions on a Euclidean Space

Smooth vs. Analytic Functions

We denote the coordinates on ${\mathbb{R}}^n$ as $x^1,\dots ,x^n$ and a point $p=(p^1,\dots ,p^n)$.

Def

A real-valued function $f:U\to \mathbb{R}$ is said to be $C^k$ at $p\in U$ if its partial derivatives

$$\frac{{\partial }^{j}f}{\partial x^{i_1}\cdots \partial x^{i_j}}$$

of all orders $j\le k$ exist and are continuous at $p$. It is $C^{\infty }$ or smooth if it is $C^k$ for all $k\ge 0$.

Some examples include:

1. Polynomials are $C^{\infty }$ over $\mathbb{R}$
2. The function $f:\mathbb{R}\to \mathbb{R}$ given by $f(x)=x^{1/3}$ is $C^0$ but not $C^1$ at $x=0$.
3. The function $g:\mathbb{R}\to \mathbb{R}$ given by $g(x)=\frac{3}{4}{x}^{4/3}$ has derivative $g^{\prime }(x)=f(x)=x^{1/3}$, so $g$ is $C^1$ but not $C^2$ at $x=0$.

We define a neighborhood of a point in ${\mathbb{R}}^n$ to be an open set containing the point. A function $f$ is real-analytic at $p$ if in a neighborhood of $p$ it is equal to it’s Taylor series at $p$:

$$f(x)=f(p)+\sum _i\frac{\partial f}{\partial x^i}(p)(x^i-p^i)+\frac{1}{2!}\sum _{i,j}\frac{{\partial }^{2}f}{\partial x^i\partial x^j}(p)(x^i-p^i)(x^j-p^j)+\dots .$$

All real-analytic functions are necessarily $C^{\infty }$ because the convergent power series can be differentiated. For example, if

$$f(x)=\sin x=x-\frac{1}{3!}{x}^3+\frac{1}{5!}{x}^5-\cdots$$

then we can differentiate to get

$$f^{\prime }(x)=\cos x=1-\frac{1}{2!}{x}^2+\frac{1}{4!}{x}^4-\cdots$$

However, not all $C^{\infty }$ functions are real-analytic. For example consider the function

$$f(x)=\{\begin{array}{ll}{e}^{-1/x}& \text{if }x>0\\ 0& \text{if }x\le 0.\end{array}$$

Notice that for $x>0$

$$\begin{array}{rl}{f}^{\prime }(x)& =\frac{e^{-1/x}}{x^2}\\ f^{\prime \prime }(x)& =\frac{e^{-1/x}(1-2x)}{x^4}\\ f^{\prime \prime \prime }(x)& =\frac{e^{-1/x}(6x^2-6x+1)}{x^6}\\ & ⋮\\ f^{(k)}(x)& =e^{-1/x}{p}_{2k}(1/x)\text{ for some polynomial }{p}_{2k}\text{ of degree }2k.\end{array}$$

Thus, if we let $x\to 0$, (making use of L’Hopital’s rule)

$$\begin{array}{rl}\underset{x\to 0}{\lim }{e}^{-1/x}{p}_{2k}(1/x)& =\underset{x\to 0}{\lim }\frac{p_{2k}(1/x)}{e^{1/x}}\\ & =\underset{x\to 0}{\lim }\frac{p_{2k-1}(1/x)}{e^{1/x}}\\ & ⋮\\ & =\underset{x\to 0}{\lim }\frac{0}{e^{1/x}}=0.\end{array}$$

Hence, $f^{(k)}=0$ for all $k\ge 0$. Therefore, $f$ is $C^{\infty }$ but the Taylor series at the origin is zero in every neighborhood, i.e., $f$ is not real-analytic.

Taylor’s Theorem with Remainder

We say a subset $S\subset {\mathbb{R}}^n$ is star-shaped with respect to $p\in S$ if for every $x\in S$, the line segment from $p$ to $x$ lies in $S$. For example:

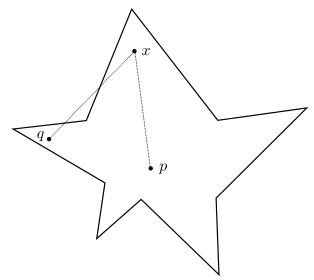
The set $S$ is star-shaped with respect to $p$, but not $q$.

Taylor's theorem with remainder

Let $f$ be a $C^{\infty }$ function on an open subset $U$ of ${\mathbb{R}}^n$ star-shaped with respect to a point $p=(p^1,\dots ,p^n)$ in $U$. Then there are functions $g_1(x),\dots ,g_n(x)\in C^{\infty }(U)$ such that

$$f(x)=f(p)+\sum _{i=1}^n(x^i-p^i)g_i(x),g_i(p)=\frac{\partial f}{\partial x^i}(p).$$

Proof: Notice that for any $x\in U$ the line segment $p+t(x-p)$, $0\le t\le 1$ lies in $U$ since $U$ is star-shaped with respect to $p$. If we differentiate using the chain rule

$$\frac{d}{dt}f(p+t(x-p))=\sum (x^i-p^i)\frac{\partial f}{\partial x^i}(p+t(x-p)).$$

If we integrate both sides from 0 to 1,

$$f(p+t(x-p)){|}_0^1=\sum (x^i-p^i){\int }_0^1\frac{\partial f}{\partial x^i}(p+t(x-p))dt.$$

Letting

$$g_i(x)={\int }_0^1\frac{\partial f}{\partial x^i}(p+t(x-p))$$

gives the result.

Problems

1.3. A diffeomorphism of an open interval with $\mathbb{R}$

Let $U\subset {\mathbb{R}}^n$ and $V\subset {\mathbb{R}}^n$ be open intervals. A $C^{\infty }$ map $F:U\to V$ is called a diffeomorphism if it is bijective and has a $C^{\infty }$ inverse $F^{-1}:V\to U$. Show that any two finite intervals are diffeomorphic.

Answer: Let $a<b$ and define $f:(0,1)\to (a,b)$ by $f(t)=ta+(1-t)b$. Notice that $f$ is $C^{\infty }(0,1)$ since

$$\begin{array}{rl}{f}^{\prime }(t)& =a-b\\ f^{\prime \prime }(t)& =0\end{array}$$

are continuous. Moreover, $f$ is bijective with inverse

$$f^{-1}(x)=\frac{x-b}{a-b}$$

and

$$\frac{d}{dx}{f}^{-1}(x)=\frac{1}{a-b}\text{ and }\frac{d^2}{d{x}^2}{f}^{-1}(x)=0.$$

Therefore, $f$ is a diffeomorphism. Since $a$ and $b$ are arbitrary, it follows that all finite intervals $(a,b)$ are diffeomorphic.

1.5. A diffeomorphism of an open ball with ${\mathbb{R}}^n$

Let $\text{0}=(0,0)$ be the origin and $B(\text{0},1)$ be the open unit disk in ${\mathbb{R}}^2$. To find a diffeomorphism between $B(\text{0},1)$ and ${\mathbb{R}}^2$, we identify ${\mathbb{R}}^2$ with the $xy$-plane in ${\mathbb{R}}^3$ and introduce the lower open hemisphere

$$S:x^2+y^2+(z-1{)}^2=1,z<1,$$

in ${\mathbb{R}}^3$ as an intermediate space. Note that the map

$$f:B(\text{0},1)\to S,(a,b)\mapsto (a,b,1-\sqrt{1-a^2-b^2})$$

is a bijection.

(a) The stereographic projection $g:S\to {\mathbb{R}}^2$ from $(0,0,1)$ is the map that sends a point $(a,b,c)\in S$ to the intersection of the line through $(0,0,1)$ and $(a,b,c)$ with the $xy$-plane. Determine the map $g$ and it’s inverse.

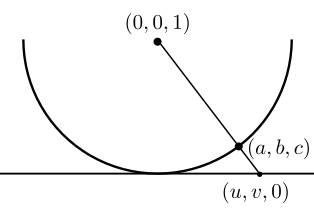
Answer: We seek the map $(a,b,c)\mapsto (u,v)$ for $(a,b,c)\in S$. By similar triangles (working in the $xz$-plane), notice that

$$\frac{u-a}{c}=\frac{u}{1}.$$

Solving for $u$ we get that $u=a/(1-c)$. We repeat this in the $yz$-plane to get $v=b/(1-c)$. Therefore, $g$ is given by

$$(a,b,c)\mapsto \left(\frac{a}{1-c},\frac{b}{1-c}\right).$$

We now seek the inverse map $g^{-1}$. Notice that $(a,b,c)\in S$ implies that $c=1-\sqrt{1-a^2-b^2}$. Hence, solving for $a$ and $b$ gives us

$$(u,v)\mapsto \left(\frac{u}{\sqrt{1+u^2+v^2}},\frac{v}{\sqrt{1+u^2+v^2}},1-\frac{1}{\sqrt{1+u^2+v^2}}\right).$$

(b) Composing the two maps $f$ and $g$ gives the map

$$h=g\circ f:B(\text{0},1)\to {\mathbb{R}}^2,h(a,b)=\left(\frac{a}{\sqrt{1-a^2-b^2}},\frac{b}{\sqrt{1-a^2-b^2}}\right).$$

Find the formula for $h^{-1}(u,v)$ and conclude that $h$ is a diffeomorphism of the open disk $B(\text{0},1)$ with ${\mathbb{R}}^2$.

Answer: Notice that

$$\begin{array}{rl}{h}^{-1}(u,v)& =(f^{-1}\circ g^{-1})(u,v)\\ & =f^{-1}\left(\frac{u}{\sqrt{1+u^2+v^2}},\frac{v}{\sqrt{1+u^2+v^2}},1-\frac{1}{\sqrt{1+u^2+v^2}}\right)\\ & =\left(\frac{u}{\sqrt{1+u^2+v^2}},\frac{v}{\sqrt{1+u^2+v^2}}\right)\end{array}$$

One may verify that $h$ and $h^{-1}$ are $C^{\infty }$.