2024-03-26

For problem 3 on the computational topology homework, I’m trying to find a pair of spaces that have the same homology groups, but are not homotopy equivalent. After talking to Patrick he mentioned comparing the torus and $S^1\vee S^1\vee S^2$.

After computing their corresponding Betti numbers over ${\mathbb{Z}}_2$, I found that for both the torus and $S^1\vee S^1\vee S^2$ the homology groups are

$$H_0\cong {\mathbb{Z}}_2,H_1\cong {\mathbb{Z}}_2\oplus {\mathbb{Z}}_2,H_2\cong {\mathbb{Z}}_2.$$

Which just leaves proving that they are not homotopy equivalent.

Patrick thinks you can do it by looking at the homotopy groups. While we haven’t covered homotopy groups in class, I feel it is worth a try. Primarily by showing that the fundamental groups ${\pi }_1$ are not isomorphic.

The following notes are from reading the Wikipedia page on the fundamental group: https://en.wikipedia.org/wiki/Fundamental_group.

Fundamental Group

Given a topological space $X$, we define a loop based at $x_0$ to be a continuous map $\gamma :[0,1]\to x$ such that $\gamma (0)=\gamma (1)=x_0$. Then a homotopy between two loops $\gamma ,{\gamma }^{\prime }$ (both based at $x_0$) would be a map $H:[0,1]\times [0,1]\to X$ such that $H(r,0)=\gamma (r)$ and $H(r,1)={\gamma }^{\prime }(r)$ for all $r\in [0,1]$. If such a map exists, then $\gamma$ and ${\gamma }^{\prime }$ are homotopy equivalent, denoted $\gamma \sim {\gamma }^{\prime }$.

The fundamental group is given by the equivalence classes of loops based at $x_0$.

Fundamental Group

$${\pi }_1(X,x_0)=\{\text{loops γ based around x0}\}/\sim$$

where $\sim$ is homotopy equivalence.

Looking at the name fundamental group suggests this set is a group. We define the product of two loops $\gamma ,{\gamma }^{\prime }$ as a new loop $\gamma \cdot {\gamma }^{\prime }:[0,1]\to X$ given by

$$(\gamma \cdot {\gamma }^{\prime })(t)=\{\begin{array}{ll}\gamma (2t)& 0\le t\le 1/2\\ {\gamma }^{\prime }(2t-1)& 1/2\le t\le 1.\end{array}$$

In other words, we follow loop $\gamma$ twice as fast then follow ${\gamma }^{\prime }$ twice as fast. Thus, the fundamental group has product $[\gamma \cdot {\gamma }^{\prime }]$ for two equivalence classes $[\gamma ],[{\gamma }^{\prime }]\in {\pi }_1(X,x_0)$. One may show this operator satisfies the group requirements.

Fundamental Group of Circle

Let $x_0\in S^1$. Notice that any loop $\gamma :[0,1]\to S^1$ based at $x_0$ simply starts at $x_0$ then goes along the circle $m$ times before stopping at $x_0$.

Thus, for a loop ${\gamma }_m$ that revolves $m$-times and a loop ${\gamma }_n$ that revolves $n$-times, the product ${\gamma }_m\cdot {\gamma }_n$ revolves $(m+n)$-times. Therefore, one can see that ${\pi }_1(S^1,x_0)\cong \mathbb{Z}$.

Fundamental Group of 2-Sphere

Let $x_0\in S^2$ and consider any loop $\gamma :[0,1]\to S^2$ based at $x_0$. Then one may show that the image of $\gamma$ is contractible. That is, $\gamma$ is homotopy equivalent to the trivial loop. Therefore, the fundamental group ${\pi }_1(S^2,x_0)$ is trivial.

Fundamental Group of Products and Coproducts

Let $f:X\to Y$ be a continuous map between topological spaces. Let $x_0\in X$ and $y_0=f(x_0)$. If we take any loop $\gamma$ with base point $x_0$ in $X$, we can compose with $f$ to get a loop $f\circ \gamma$ with base point $y_0$ in $Y$. One may show that this induces a homomorphism

$$f_{\ast }:{\pi }_1(X,x_0)\to {\pi }_1(Y,y_0)$$

between fundamental groups.

This pattern gives a rise to the fundamental group functor $(X,x_0)\mapsto {\pi }_1(X,x_0)$.

One consequence of this is that two homotopy equivalent path-connected spaces have isomorphic fundamental groups. Or more importantly for solving problem 3, two spaces with different fundamental groups are not homotopy equivalent.

The fundamental group functor can be shown to map products to products and coproducts to coproducts. Therefore, if $X$ and $Y$ are path connected, then

$${\pi }_1(X\times Y,(x_0,y_0))\cong {\pi }_1(X,x_0)\times {\pi }_1(Y,y_0)$$

and if they are locally contractible on top of that,

$${\pi }_1(X\vee Y)\cong {\pi }_1(X)\ast {\pi }_1(Y)$$

where $\ast$ represents the free product of groups.

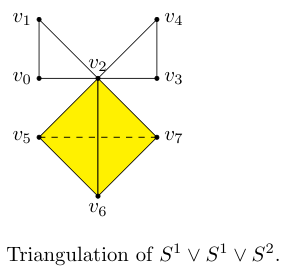
Solving Problem 3

Given the above, the torus $T^2=S^1\times S^1$ has fundamental group $\mathbb{Z}\times \mathbb{Z}$ and the wedge sum $S^1\vee S^1\vee S^2$ has fundamental group $\mathbb{Z}\ast \mathbb{Z}$. If we look at the representations, we see that

$$\mathbb{Z}\times \mathbb{Z}=⟨a,b\mid ab=ba⟩\text{ and }\mathbb{Z}\ast \mathbb{Z}=⟨a,b⟩$$

which are not isomorphic.