2025-08-21

R-Trees

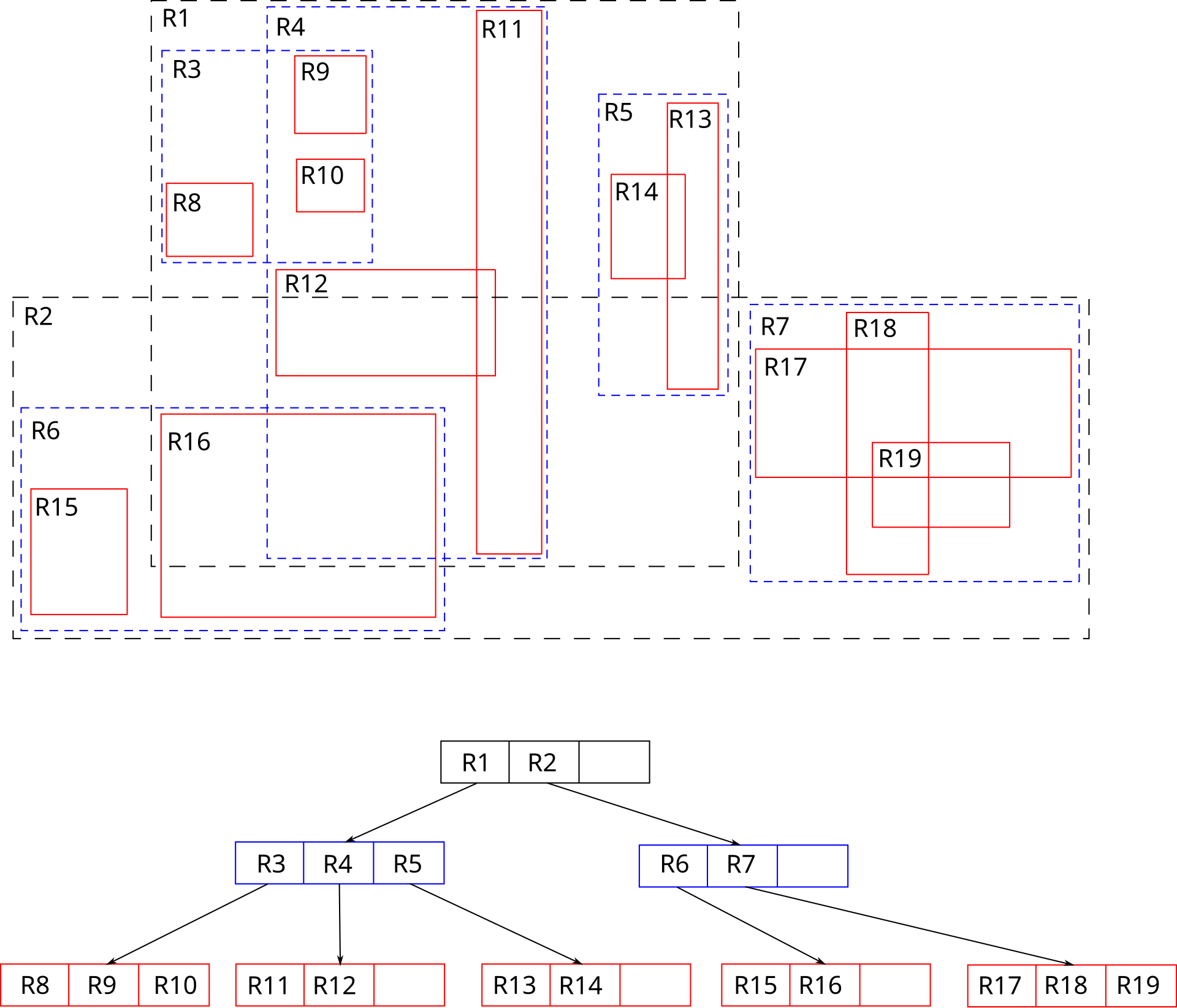
• Each node of the tree has at most $M=32$ entries.
• Each entry represents a rectangle.
• The entries for the leafs have a net ID and that net’s bounding box as its rectangle
• Each leaf is given a omp_lock_t

Parallel Algorithm:

• For each net $N$:
  • Find the leaf that net $N$ belongs to
  • Set the leafs lock
  • Solve the net
  • Unset the leafs lock

\newpage

R-Tree Construction Methods

I investigated four different R-tree construction methods.

Quadratic

• Original method by Guttman (1984)
• Online method - entries inserted one at a time

Algorithm:

1. Find the leaf in which the smallest change in rectangle size for new entry and insert the entry.
2. If there is no room left in the leaf, split the leaf:
   1. Find two entries which would have the largest MBR if in the same node. Use them to create two leafs $L$ and $R$.
   2. While there are remaining entries
      1. Pick the entry that causes the largest difference in MBR size between $L$ and $R$ (maximize $|\Delta L-\Delta R|$). Insert into $L$/$R$ based on whatever the smallest change in size is.

Hilbert/Z-Order

• Bulk method by Kamel and Faloutsos (1993)
• Makes use of a space-filling curve
• Leaves may overlap

Algorithm:

1. Construct $P=\lceil n/M\rceil$ new nodes
2. Sort the rectangles via a space-filling curve
3. Pack the rectangles into the $P$ nodes in order
   1. Node 1 gets first $M$ rectangles, node 2 gets second $M$ rectangles, etc.
4. Repeat the process until you obtain a root node

Sort-Tile-Recursive (STR)

• Bulk method by Leuteneggaer et al. (1997)
• Goal is to have the leaf nodes tile the space
  • Tiling is only guaranteed for point data

Algorithm:

1. Construct $P=\lceil n/M\rceil$ new nodes.
2. Sort the rectangles by centers $x$-coordinate and partition into $S=\lceil \sqrt{P}\rceil$ slices consisting of at most $S\cdot M$ consecutive rectangles
3. Sort each slice by rectangles $y$-coordinate
4. Pack the rectangles into the $P$ nodes in order
5. Repeat the process until you obtain a root node

\newpage