2024-08-23

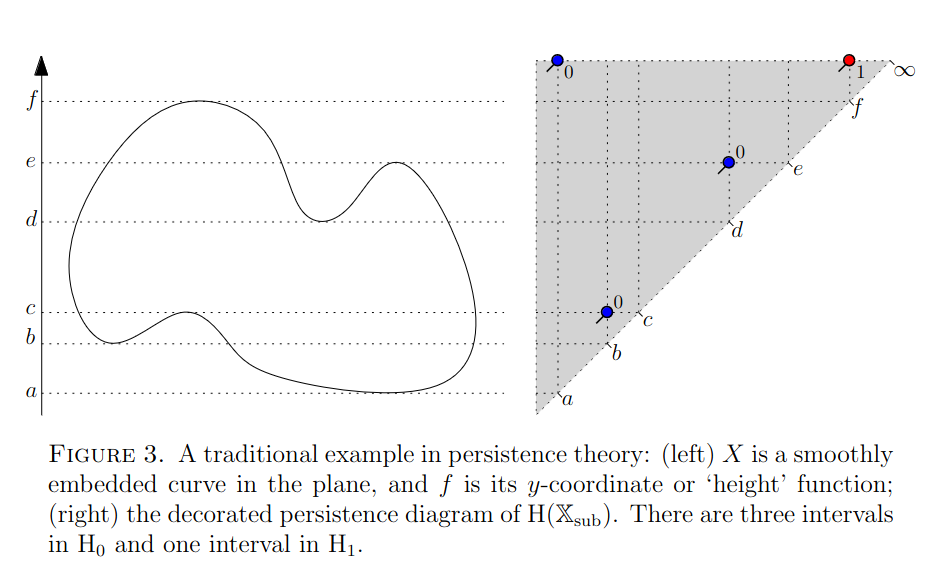
The paper The structure and stability of persistence modules often uses a sublevelset filtration as examples. These notes are an exploration of persistence homology of sublevelsets.

Singular Homology

We define the standard $n$-simplex to to be the $n$-simplex given by the $n+1$ vertices

$$\begin{array}{rl}{e}_0& =(1,0,\dots ,0)\\ e_1& =(0,1,\dots ,0)\\ & ⋮\\ e_n& =(0,0,\dots ,1)\end{array}$$

Let $X$ be a topological space. A singular $n$-simplex is a continuous function (map) $\sigma :{\Delta }^n\to X$. This map does not have to be injective. Moreover, two non-equivalent singular simplices may have the same image. We often designate $\sigma$ by its vertices

$$[v_0,v_1,\dots ,v_n]=[\sigma (v_0),\sigma (v_1),\dots ,\sigma (v_n)].$$

Under this, we can define homology groups as in Homology Groups. That is, we define a singular $p$-chain to be a weighted sum of singular $p$-simplices

$$c=\sum _{i=1}^m{a}_i{\sigma }_i$$

where $a_i$ are coefficients from a group (typically ${\mathbb{Z}}_2)$. Then the boundary map $\partial :C_p\to C_{p-1}$, where $C_p$ is the set of singular $p$-chains, is given by

$$\partial c=\sum _{i=1}^m{a}_i\partial {\sigma }_i$$

where

$$\partial \sigma =\partial [v_0,v_1,\dots ,v_p]=\sum _{k=0}^p(-1{)}^k[v_0,\dots ,v_{k-1},v_{k+1},\dots ,v_p].$$

Under the boundary map, we get a chain complex of abelian groups called the singular complex

$$\cdots \to C_{p+1}\to C_p\to C_{p-1}\to \cdots$$

We define the $n$-th singular homology class as the quotient

$$H_n(X)=\text{Ker}({\partial }_n)/\text{Im}({\partial }_{n+1}).$$

Sublevelset Persistence

Let $X$ be a topological space and let $f:X\to \mathbb{R}$ be a function. We define a sublevel set to be the set

$$X^t=(X,f{)}^t=\{x\in X\mid f(x)\le t\}.$$

Under the inclusion maps $i_s^t:X^s\hookrightarrow X^t$ for $s\le t$, we can form the sublevelset filtration of $(X,f)$,

$${\mathbb{X}}_{\text{sub}}^f:X^{t_1}\to X^{t_2}\to X^{t_3}\to \cdots$$

We can define a persistence module of taking the $p$-dimensional singular homology with coefficients in $k$. That is, we define $\mathbb{V}$ by letting

$$V_t=H(X^t)$$

and

$$v_s^t=H(i_s^t):H(X^s)\to H(X^t).$$

One may show that the vector spaces $H(X^t)$ are finite-dimensional. More over, as $t$ increases there are a finite number of “critical values” where the complex changes. Thus, if $a_1<a_2<\cdots <a_n$ are said critical values, then we get the persistence module

$$\mathbb{V}:H(X^{a_1})\to H(X^{a_2})\to \cdots \to H(X^{a_n}).$$

For example: