A. Point-Set Topology

Topology

A topology on a set $S$ is a collection $\mathcal{T}$ of subsets such that

1. $\varnothing ,S\in \mathcal{T}$
2. (Arbitrary union) if $U_a\in \mathcal{T}$ for all $a\in A$, then ${\bigcup }_{a\in A}{U}_a\in \mathcal{T}$
3. (Finite intersection) if $U_1,\dots ,U_n\in \mathcal{T}$, then $U_1\cap \cdots \cap U_n\in \mathcal{T}$.

We call elements of a topology open sets and the pair $(S,\mathcal{T})$ a topological space. A neighborhood of a point $p\in S$ is an open set $U$ that contains $p$.

Example: The standard topology for ${\mathbb{R}}^n$ consists of sets $U$ that are open if and only if for every $p\in U$, there is a open ball $B(p,ϵ)$ with center $p$ and radius $ϵ$ contained in $U$.

If ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ are both topologies of $S$ and ${\mathcal{T}}_1\subset {\mathcal{T}}_2$, then we say that ${\mathcal{T}}_2$ is finer than ${\mathcal{T}}_1$. Or equivalently, ${\mathcal{T}}_1$ is coarser than ${\mathcal{T}}_2$.

Local criterion for openness

Let $S$ be a topological space. A subset $A$ is open in $S$ if and only if for every $p\in A$, there is an open set $V$ such that $p\in V\subseteq A$.

Proof: ($\Rightarrow$): Clearly $p\in A\subseteq A$ for all $p\in A$. ($\Leftarrow$): Notice that for each $p\in A$ there is a open set $V_p\subset A$. But,

$$A=\bigcup _{p\in A}{V}_p$$

and the arbitrary union of open sets is open.

Q.E.D.

A set $V$ is called closed if it’s complement $S\backslash V$ is open. By the use of de Morgan’s laws, one can redefine a topology in terms of closed sets.

Topology

A topology on a set $S$ is a collection $\mathcal{T}$ of subsets such that

1. $\varnothing$ and $S$ are closed
2. (Arbitrary intersection) if $U_a$ is closed for all $a\in A$, then ${\bigcap }_{a\in A}{U}_a$ is closed.
3. (Finite union) if $U_1,\dots ,U_n$ are closed, then $U_1\cup \cdots \cup U_n$ is closed.

Subspace Topology

Let $(S,\mathcal{T})$ be a topological space and $A\subseteq S$. Define ${\mathcal{T}}_A$ to be the collection of subsets

$${\mathcal{T}}_A=\{U\cap A\mid U\in \mathcal{T}\}.$$

By the distributive property of union and intersection, one may show that ${\mathcal{T}}_A$ is closed under arbitrary union and finite intersection. Moreover, $\varnothing ,A\in {\mathcal{T}}_A$. Thus, ${\mathcal{T}}_A$ is a topology on $A$ called the subspace topology.

Example: Consider the subset $A=[0,1]$ of $\mathbb{R}$. In the subspace topology, the half-open interval $[0,1/2)$ is open relative to $A$ since

$$[0,1/2)=(-1/2,1/2)\cap A$$

and $(-1/2,1/2)$ is open in $\mathbb{R}$.

Bases

Instead of explicitly stating all the possible open sets, we often make use of the local criterion for openness and define a basis of sets.

Basis

A subcollection $\mathcal{B}$ of a topology $\mathcal{T}$ on a topological space $S$ is a basis for $\mathcal{T}$ if given an open set $U$ and a point $p\in U$, there is an open set $B\in \mathcal{B}$ such that $p\in B\subset U$. We say that $\mathcal{B}$ generates the topology $\mathcal{T}$.

Example: The standard topology for ${\mathbb{R}}^n$ is generated by the collection of open balls

$$B(p,r)=\{x\in {\mathbb{R}}^n\mid d(p,x)<r\}$$

for all $p\in {\mathbb{R}}^n$ and $r\in \mathbb{R}$.

Prp

A collection $\mathcal{B}$ of open sets of $S$ is a basis if and only if every open set in $S$ is a union of sets in $\mathcal{B}$.

Proof: ($\Rightarrow$): Let $U$ be open. Since $\mathcal{B}$ is a basis, there are open sets $V_p\in \mathcal{B}$ for each $p\in U$. Notice that

$$U=\bigcup _{p\in U}{V}_p.$$

$(\Leftarrow$): Let $U$ be open and $p\in U$. Since $U={\bigcup }_{a\in A}{V}_a$ with each $V_a\in \mathcal{B}$, there is some $a\in A$ such that $p\in V_a$. Thus, $\mathcal{B}$ is a basis.

Q.E.D.

Prp

A collection $\mathcal{B}$ of subsets of a set $S$ is a basis for some topology $\mathcal{T}$ on $S$ if and only if

1. $S$ is the union of all sets in $\mathcal{B}$; and
2. given any two sets $B_1,B_2\in \mathcal{B}$ and a point $p\in B_1\cap B_2$, there is a set $B\in \mathcal{B}$ such that $p\in B\subset B_1\cap B_2$.

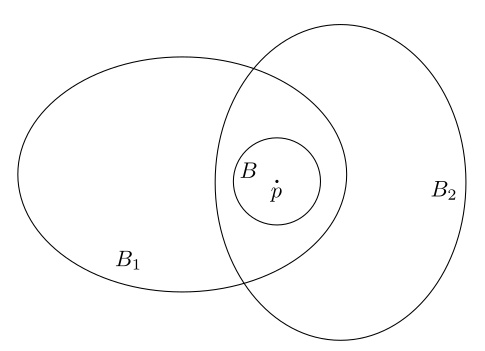
Proof: ($\Rightarrow$):

1. See previous proposition.
2. Since $\mathcal{B}$ is a basis, $B_1,B_2$ and $B_1\cap B_2$ are open. Hence, by the definition of basis, there is a $B\in \mathcal{B}$ such that $p\in B\subset B_1\cap B_2$.

($\Leftarrow$): Let $\mathcal{T}$ be the collection of all sets that unions of set sin $\mathcal{B}$. Note that $\varnothing ,S\in \mathcal{T}$. Clearly, an arbitrary union of sets in $\mathcal{T}$ is in $\mathcal{T}$. For finite intersection, let $U={\bigcup }_{\mu }{B}_{\mu }$ and $V={\bigcup }_{\nu }{B}_{\nu }$ be sets in $\mathcal{T}$. Notice that

$$U\cap V=\left(\bigcup _{\mu }{B}_{\mu }\right)\cap \left(\bigcup _{\nu }{B}_{\nu }\right)=\bigcup _{\mu ,\nu }(B_{\mu }\cap B_{\nu }).$$

Hence, for any $p\in U\cap V$, it follows that $p\in B_{\mu }\cap B_{\nu }$ for some $\mu ,\nu$. By property (2), there is a set $B_p\in \mathcal{B}$ such that $p\in B_p\subset B_{\mu }\cap B_{\nu }$. Therefore,

$$U\cap V=\bigcup _{p\in U\cap V}{B}_p.$$

Hence, $\mathcal{T}$ is a topology.

Q.E.D.

Prp

Let $\mathcal{B}=\{B_{\alpha }\}$ be a basis for a topological space $S$, and $A$ a subspace of $S$. Then $\{B_{\alpha }\cap A\}$ is a basis for $A$.

Proof: Let $U$ be open relative to $A$, i.e., $U=U^{\prime }\cap A$ for some open set $U^{\prime }$ in $S$. Since $\mathcal{B}$ is a basis for $S$, it follows that $U^{\prime }={\bigcup }_{\mu }{B}_{\mu }$. Notice that

$$U=\left(\bigcup _{\mu }{B}_{\mu }\right)\cap A=\bigcup _{\mu }(B_{\mu }\cap A).$$

Q.E.D.

First and Second Countability

Second countable

A topological space is second countable if it has a countable basis.

Example: ${\mathbb{R}}^n$ is second countable since it is generated by the collection of open balls in ${\mathbb{R}}^n$ with rational centers and rational radii.

Prp

A subspace $A$ of a second-countable space $S$ is second countable.

Proof: Follows from proposition 7.

Q.E.D.

First Countable

Let $S$ be a topological space and $p\in S$. A basis of neighborhoods at $p$ is a collection $\mathcal{B}=\{B_{\alpha }\}$ of neighborhoods of $p$ such that any neighborhood $U$ of $p$, there is a $B_{\alpha }\in \mathcal{B}$ such that $p\in B_{\alpha }\subseteq U$. A topological space $S$ is first countable if it has a countable basis of neighborhoods at every point $p\in S$.

Example: For any $p\in {\mathbb{R}}^n$, the collection $\{B(p,1/n){\}}_{n=1}^{\infty }$ is a countable neighborhood basis at $p$. Thus, ${\mathbb{R}}^n$ is first countable.

Example: An uncountable discrete space is first countable but not second countable.

Separation Axioms

Hausdorff

A topological space $S$ is Hausdorff if given any two distinct points $x,y\in S$, there exists disjoint open sets $U,V$ such that $x\in U$ and $y\in V$. A Hausdorff space is normal if given any two distinct closed sets $F,G$ in $S$, there exists disjoint open sets $U,V$ such that $F\subset U$ and $G\subset V$.

Example: ${\mathbb{R}}^n$ is Hausdorff since any two distinct points can be put in disjoint balls $B(x,ϵ)$ and $B(y,ϵ$) for $ϵ=d(x,y)/2$. Moreover, it is also normal.

Prp

Every singleton set in a Hausdorff space $S$ is closed.

Proof: Let $x\in S$. Notice that for any $y\in S\setminus \{x\}$ there is open sets $U$ and $V$ such that $U\cap V=\varnothing$, $x\in U$ and $y\in V$. Notice that $V\subseteq S\setminus U\subseteq S\setminus \{x\}$. Therefore, $S\setminus \{x\}$ is open implying that $\{x\}$ is closed.

Q.E.D.

Prp

Any subspace $A$ of a Hausdorff space $S$ is Hausdorff.

Proof: Let $x,y\in A$ be distinct points. Then $x,y\in S$ so there are disjoint open sets $U$ and $V$ such that $x\in U$ and $y\in V$. Notice that $x\in U\cap A$, $y\in V\cap A$ and

$$(U\cap A)\cap (V\cap A)=(U\cap V)\cap A\subseteq U\cap V=\varnothing .$$

Therefore, $A$ is Hausdorff.

Q.E.D.

Product Topology

Given two topological spaces $X,Y$. Consider the collection $\mathcal{B}$ of subsets of $X\times Y$ where $U\subset X$ is open in $X$ and $V\subset Y$ is open in $Y$. Then $\mathcal{B}$ is the basis for a topology on $X\times Y$ known as the product topology.

Prp

Let $\{U_i\}$ and $\{V_i\}$ be bases for topological spaces $X$ and $Y$, respectively. Then $\{U_i\times V_j\}$ is a basis for $X\times Y$.

Proof: Let $W$ be open in $X\times Y$ and $(x,y)\in W$. Since $W$ is open, there is an open set $U\times V$ in $X\times Y$ such that $(x,y)\in U\times V\subseteq W$ where $U$ is open in $X$ and $V$ is open in $Y$. Notice that there is some $i$ such that $x\in U_i\subset U$ and $j$ such that $y\in V_j\subset V$. Therefore,

$$(x,y)\in U_i\times V_j\subset U\times V\subset W.$$

Therefore, $\{U_i\times V_j\}$ is a basis for $X\times Y$.

Q.E.D.

Example: The collection of open rectangles $(a,b)\times (c,d)$ is a basis for ${\mathbb{R}}^2=\mathbb{R}\times \mathbb{R}$.

Cor

The product of two second-countable spaces is second-countable.

Prp

The product of two Hausdorff spaces $X$ and $Y$ is Hausdorff.

Proof: Let $(x_1,y_1),(x_2,y_2)\in X\times Y$. WLOG, assume that $x_1\ne x_2$. Since $X$ is Hausdorff, there are disjoint open sets $U_1,U_2\in X$ such that $x_1\in U_1$ and $x_2\in U_2$. Notice that $U_1\times Y$ and $U_2\times Y$ are disjoint neighborhoods of $(x_1,y_1)$ and $(x_2,y_2)$, respectively.

Q.E.D.

Continuity

Let $f:X\to Y$ be a function between topological spaces. We say that $f$ is continuous at a point $p$ in $X$ if for every neighborhood $V$ of $f(p)$ in $Y$, there is a neighborhood $U$ of $p$ in $X$ such that $f(U)\subset V$.

Prp

A function $f:X\to Y$ is continous if and only if $f^{-1}(V)$ is open for any open set $V$.

Cor

A function $f:X\to Y$ is continuous if and only if $f^{-1}(V)$ is closed for any closed set $V$.

Example: If $A$ is a subspace of $X$, then the inclusion map $i:A\hookrightarrow X$, $i(a)=a$, is continuous. Indeed, if $U$ is open in $X$, then $i^{-1}(U)=U\cap A$ is open in $A$.

Example: The projection map $\pi :X\times Y\to X$ given by $\pi (x,y)=x$ is continuous. Indeed, if $U$ is open in $X$, then ${\pi }^{-1}(U)=U\times Y$ is open in $X\times Y$.

Prp

The composition of two continuous maps is continuous.

Proof: Let $f:X\to Y$ and $g:Y\to Z$ be continuous. Then for $U$ open in $Z$,

$$(f\circ g{)}^{-1}(U)=g^{-1}(f^{-1}(U))$$

is open in $X$ since $f^{-1}(U)$ is open in $Y$.

Q.E.D.

Cor

The restriction $f{|}_A$ of a continuous function $f:X\to Y$ to a subspace $A$ is continuous.

Proof: The restriction $f{|}_A$ is the composition $f\circ i$ where $i:A\hookrightarrow X$ is the inclusion map.

Q.E.D.

We call a map $f:X\to Y$ open if the image of every open set in $X$ is open in $Y$. Likewise, it is called closed if the image of every closed set in $X$ is closed in $Y$.

Compactness

We call a collection $\{U_{\alpha }\}$ of open sets an open cover of $S$ if $S\subset {\bigcup }_{\alpha }{U}_{\alpha }$. A subcover is a subcollection of an open cover that still contains $S$. We say a topological space is compact if every open cover has a finite subcover.

Example: Any closed interval $[a,b]\subset \mathbb{R}$ is compact.

Prp

A subspace $A$ of a topological space $S$ is compact if and only if every open cover of $A$ in $S$ has a finite subcover.

Prp

A closed subset $F$ of a compact topological space $S$ is compact.

Proof: Let $\{U_{\alpha }\}$ be an open cover of $F$. Notice then that $\{U_{\alpha }\}\cup \{S\backslash F\}$ is a open cover of $S$. Since $S$ is compact, there is a finite subcover $U_1,\dots ,U_n,S\backslash F$. Thus, $F\subset \bigcup U_i$.

Q.E.D.

Prp

In a Hausdorff space $S$, it is possible to separate a compact subset $K$ and a point $p\notin K$ by disjoint open sets, i.e., there exists an open set $U\supset K$ and a neighborhood $V$ of $p$ such that $U\cap V=\varnothing$.

Proof: Since $S$ is Hausdorff, for each $x\in K$ there are disjoint neighborhoods $U_x$ of $x$ and $V_x$ of $p$. Notice that $\{U_x\}$ forms an open cover of $K$, hence there is a finite subcover $U_{x_1},\dots ,U_{x_n}$. Let $U=\bigcup U_{x_i}$ and $V=\bigcap V_{x_i}$. Notice that $U$ is open and $K\subset U$. Moreover $V$ is open and $p\in V$ since each $V_i$ contains $p$. Notice that

$$U\cap V=\bigcup _i(U_{x_i}\cap V)=\bigcup _i\varnothing =\varnothing .$$

Q.E.D.

Prp

Every compact subset $K$ of a Hausdorff space $S$ is closed.

Proof: Let $p\in S\setminus K$. By the previous proposition, there is an open set $V$ containing $p$ such that $V\cap K=\varnothing$. Thus, $S\setminus K$ is open.

Q.E.D.

Prp

The image of a compact set under a continuous map is compact.

Proof: Let $f:X\to Y$ be a continuous map and $K$ a compact subset of $X$. Consider an open cover $\{V_{\alpha }\}$ of $f(K)$. Since $f$ is continuous, $\{f^{-1}(V_{\alpha })\}$ is a collection of open sets in $X$. Notice that

$$\bigcup _{\alpha }{f}^{-1}(V_{\alpha })=f^{-1}\left(\bigcup _{\alpha }{V}_{\alpha }\right)\supset f^{-1}(f(K))\supset K$$

Thus, there is a finite subcover $\{f^{-1}(V_1),\dots ,f^{-1}(V_n)\}$ of $K$. Notice that

$$\bigcup _{i=1}^{n}f(f^{-1}(V_i))=f\left(\bigcup _{i=1}^n{f}^{-1}(V_i)\right)\supset f(K).$$

Q.E.D.

Prp

A continuous map $f:X\to Y$ from a compact space $X$ to a Haudorff space $Y$ is a closed map.

Proof: Let $F$ be closed in $X$. By proposition 22, $F$ is compact. By proposition 25, $f(F)$ is compact. By proposition 24, $f(F)$ is closed.

Q.E.D.

A continuous bijection $f:X\to Y$ whose inverse is also continuous is called a homeomorphism.

Cor

A continuous bijection $f:X\to Y$ from a compact space $X$ to a Hausdorff space $Y$ is a homeomorphism.

Thm

The product of compact spaces is compact in the product topology.

Boundedness in ${\mathbb{R}}^n$

A subset $A$ of ${\mathbb{R}}^n$ is called bounded if there is an open ball $B(p,r)$ containing $A$. Otherwise it is unbounded.

Prp

A compact subset of ${\mathbb{R}}^n$ is bounded.

Proof: Let $K$ be a compact subset and consider the open cover $\{B(0,r){\}}_{r=1}^{\infty }$ of $K$. Since $K$ is compact, it follows that $K$ is contained in a single ball $B(0,r^{\prime })$.

Q.E.D.

Heine-Borel

A subset of ${\mathbb{R}}^n$ is compact if and only if it is closed and bounded.

Connectedness

Connected/Disconnected

A topological space $S$ is disconnected if it is the union $S=U\cup V$ of two disjoint nonempty open subsets $U$ and $V$. It is connected if it is not disconnected.

A subset $A$ is disconnected if it is disconnected in the subspace topology.

Prp

A subset $A$ of a topological space $S$ is disconnected if and only if there are open sets $U$ and $V$ in $S$ such that

1. $U\cap A\ne \varnothing ,V\cap A\ne \varnothing$
2. $U\cap V\cap A=\varnothing$
3. $A\subset U\cup V$

A pair of open sets in $S$ with these properties is called a separation of $A$.

Proof: $(\Rightarrow$): If $A$ is disconnected, then there are disjoint non-empty open sets $U$ and $V$ such that $A=U\cup V$. Thus, there are open sets $U^{\prime },V^{\prime }$ in $S$ such that $U=U^{\prime }\cap A$, $V=V^{\prime }\cap A$. Notice that

$$\varnothing =U\cap V=(U^{\prime }\cap A)\cap (V^{\prime }\cap A)=U^{\prime }\cap V^{\prime }\cap A$$

and

$$A=U\cup V=(U^{\prime }\cap A)\cup (V^{\prime }\cap A)\subset U^{\prime }\cup V^{\prime }.$$

($\Leftarrow$): Let $U^{\prime }=U\cap A$ and $V^{\prime }=V\cap A$. Notice that $U^{\prime },V^{\prime }$ are open in $A$,

$$U^{\prime }\cap V^{\prime }=(U\cap A)\cap (V\cap A)=\varnothing$$

and

$$U^{\prime }\cup V^{\prime }=(U\cap A)\cup (V\cup A)=(U\cup V)\cap A=A.$$

Q.E.D.

Prp

The image of a connected space $X$ under a continuous map $f:X\to Y$ is connected.

Closure

Let $S$ be a topological space and $A$ a subset of $S$. The closure of $A$ in $S$, denoted $\overline{A}$ or $\text{cl}(A)$, is defined to be the intersection of all closed sets containing $A$. In other words, it is the smallest closed set containing $A$.

Example: The closure of the open disk $B(0,r)$ in ${\mathbb{R}}^2$ is the closed disk

$$\overline{B}(0,r)=\{p\in {\mathbb{R}}^2\mid d(p,0)\le r\}.$$

Prp

Let $A$ be a subset of a topological space $S$. A point $p\in S$ is in the closure $\text{cl}A$ if and only if every neighborhood of $p$ contains a point of $A$.

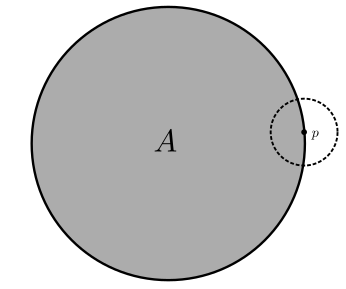
Proof: We prove the contrapositive.

$(\Rightarrow$): Suppose

$$p\notin \text{cl}(A)=\bigcap \{F\text{ closed in }S\mid F\supset A\}$$

Then $p\in S\setminus F$ for some closed set $F$ in $S$. But $S\setminus F$ is open and disjoint from $A$.

$(\Leftarrow$): Let $p$ be in a open set $U$ disjoint from $A$. Notice that then $F=S\setminus U$ is a closed set containing $A$ and not containing $p$. Thus, $p\notin \text{cl}A$.

Q.E.D.

We call a point $p\in S$ an accumulation point of $A$ if every neighborhood of $p$ in $S$ contains a point of $A$ other than $p$. We denote the set of accumulation points by $\text{ac}A$. Some texts refer to accumulation points as limit points.

Example: For $A=[0,1)\cup \{2\}$in $\mathbb{R}$, the closure of $A$ is $[0,1]\cup \{2\}$ but the set of accumulation points of $A$ is $[0,1]$.

Prp

Let $A$ be a subset of a topological space $S$. Then $\text{cl}A=A\cup \text{ac}(A)$.

Convergence

Let $S$ be a topological space. A sequence in $S$ is a map from the set $\mathbb{N}$ to $S$. We typically write $\{x_i{\}}_{i=1}^{\infty }$ or $x_1,x_2,x_3,\dots$.

We say a sequence converges to $p$ if for every neighborhood $U$ of $p$, there is some $N$ such that $n\ge N$ implies that $x_n\in U$. We often write this as $x_n\to p$ or ${\lim }_{n\to \infty }{x}_n=p$. Not every sequence converges, in such a case we say it diverges. For example the sequence $-1,1,-1,1,\dots$ in $\mathbb{R}$ diverges.

Prp

Let $S$ be a Hausdorff space. If $\{x_n\}$ converges to $p$ and to $q$, then $p=q$.

Proof: Assume $p\ne q$. Then since $S$ is Hausdorff, there are neighborhoods $U$ and $V$ of $p$ and $q$ respectively such that $U\cap V=\varnothing$. Since $x_n\to p$ there is some $N_p$ such that $x_n\in U$ whenever $n\ge N_p$. Likewise, there is some $N_q$ such that $x_n\in V$ whenever $n\ge N_q$. Then it follows that for $n\ge \max \{N_p,N_q\}$, $x_n\in U\cap V=\varnothing$.

Q.E.D.

This uniqueness property does not hold in general. The simplest counterexample is any non-empty set $X$ with the trivial topology $\mathcal{T}=\{\varnothing ,X\}$. In such a space a sequence $\{x_n\}$ converges to every point $p\in X$.

The sequence lemma

Let $S$ be a topological space and $A$ a subset of $S$. If there is a sequence $\{a_n\}$ in $A$ such that $a_n\to p$, then $p\in \text{cl}A$. The converse is true if $S$ is first countable.