Boundary Matrices

A common tool in computing reduced homology groups is boundary matrices.

Boundary Matrix

Let $K$ be a simplicial complex with $(p-1)$-simplices ${\tau }_1,\dots ,{\tau }_m$ and $p$-simplices ${\sigma }_1,\dots ,{\sigma }_n$. The p-th boundary matrix, $[{\partial }_p(K)]$, of $K$ is the $m\times n$ matrix defined by

$$[{\partial }_p(K){]}_{ij}=\{\begin{array}{ll}1& \text{if }{\tau }_i⪯{\sigma }_j\\ 0& \text{otherwise}.\end{array}$$

The above definition is when working with the underlying group of ${\mathbb{Z}}_2$. When working over $\mathbb{Z}$, the non-zero entries are $\pm 1$ depending on the orientations. For now we work over ${\mathbb{Z}}_2$. For example, consider the complex $K$ below:

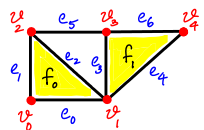
Then the 0-th boundary matrix is

$$[{\partial }_0]=\begin{array}{cc}& \begin{array}{ccccc}{v}_0& v_1& v_2& v_3& v_4\end{array}\\ \begin{array}{c}\varnothing \end{array}& \left[\begin{array}{ccccc}1& 1& 1& 1& 1\end{array}\right]\end{array}$$

and the 1-st boundary matrix would be

$$[{\partial }_1]=\begin{array}{cc}& \begin{array}{ccccccc}{e}_0& e_1& e_2& e_3& e_4& e_5& e_6\end{array}\\ \begin{array}{c}{v}_0\\ v_1\\ v_2\\ v_3\\ v_4\end{array}& \left[\begin{array}{ccccccc}1& 1& & & & & \\ 1& & 1& 1& 1& & \\ & 1& 1& & & 1& \\ & & & 1& & 1& 1\\ & & & & 1& & 1\end{array}\right]\end{array}.$$

Notice that a $p$-chain is just a sum of columns and a $(p-1)$-chain is a sum of rows. Boundary matrices get their name as they are the matrix representation of the boundary homomorphism. That is, if $c=\sum a_i{\sigma }_i$ is a $p$-chain over ${\mathbb{Z}}_2$, then ${\partial }_{p}c$ is given by the matrix-vector product $[{\partial }_p]c$.

As a result, the columns of $[{\partial }_p]$ generate the $p$-chain group $C_p$. Likewise, the rows of $[{\partial }_p]$ generate $C_{p-1}$. We can make use of boundary matrices to get generators of the boundary and cycle groups $B_p$ and $Z_p$.

Smith Normal Form

Smith Normal Form

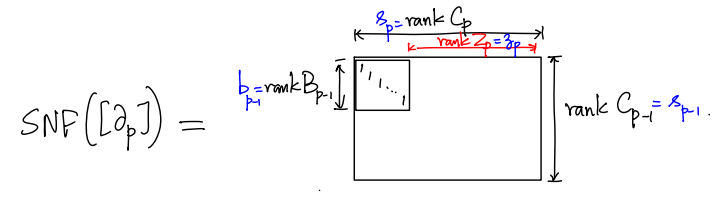
A matrix $A\in {\mathbb{Z}}^{m\times n}$ is in Smith normal form (SNF) if $A$ is of the form

$$A=\left[\begin{array}{cc}D& 0\\ 0& 0\end{array}\right]$$

where $D=\text{diag}(d_1,\dots ,d_{\ell })$ with $d_i\in \mathbb{Z}$, $d_i\ge 1$ and $d_1\mid d_2\mid \cdots \mid d_{\ell }$.

When working over ${\mathbb{Z}}_2$, we get that $D=I_{\ell }$, the $\ell \times \ell$ identity matrix.

The structure of the SNF of the boundary matrix $[{\partial }_p]$ tells us the rank of $C_p,Z_p$ and $B_{p-1}$.

For example,

$$\text{SNF}([{\partial }_1])=\left[\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$

implying that $\text{rank}{Z}_1=3$ and $\text{rank}{B}_0=4$.

Even more, the SNF is of the form

$$\text{SNF}([{\partial }_p])=U_{p-1}[{\partial }_p]V_p,$$

where $U_{p-1}$ is the product of elementary row operations and $V_p$ is the product of elementary column operations. The last $\text{rank}{Z}_p$ columns of $V_p$ encode a basis for $Z_p$ and the first $\text{rank}{B}_{p-1}$ columns of $U_{p-1}^{-1}$ encode a basis for $B_p$.

If we keep track of the row and column operations as we go, the labels for the last three columns are $e_0+e_1+e_2$, $e_0+e_1+e_3+e_5$, $e_3+e_4+e_6$. These 1-cycles form a basis for $Z_1$.

SNF Algorithm over ${\mathbb{Z}}_2$

Algorithm 1 Smith normal form of $B\in\Z_2^{m\times n}$

procedure Reduce($i$)

if $\exists j\ge i,k\ge i\text { with }B_{jk}=1$ then

$R_j\rightleftharpoons R_i$

$C_j\rightleftharpoons C_i$

for $h=i+1,\dots,m$ do

if $B_{hi}=1$ then

$R_h\leftarrow R_h+R_i$

end if

end for

for $\ell=i+1,\dots,n$ do

if $B_{i\ell}=1$ then

$C_\ell\leftarrow C_\ell+C_i$

end if

end for

Reduce($i+1$)

end if

end procedure