Steinhaus Filtration and Stable Paths in the Mapper

Questions:

• What is the problem we are trying to solve?
• What does the “birth time” of a simplex $\sigma$ mean? Answer: Smallest time $t$ such that $\sigma$ is created in the filtration.
• How to pick the intervals for Mapper construction?
• How to visualize bottleneck metric on covers?
• How does interleaved filtration relate to stability?
• Why does an isomorphism between the 1-skeleton of VR and cover imply isomorphism between filtrations?
• How to interpret Pareto frontiers?

Full paper can be found at: https://arxiv.org/abs/1906.08256.

Introduction

Two important concepts in TDA are persistentence and the Mapper construction.

It is typically unclear as to how one should interpret higher dimensional homology. One method is via persistence diagrams.

In most TDA applications we are under the assumption that the data has a metric. However, assigning a meaningful metric is not always clear, e.g., Netflix movie recommendations.

Mapper construction is defined to be the nerve of a cover of data:

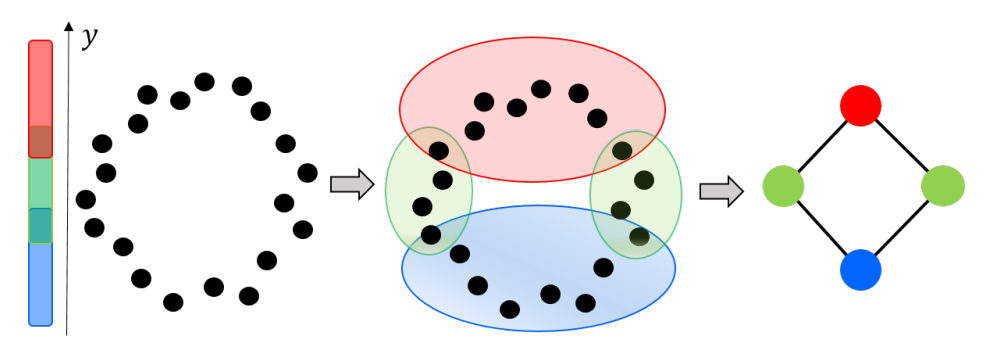
We begin with a set of overlapping intervals covering the possible values of some parameter (shown here as the $y$-axis). Next we cluster the data set such that each cluster falls into an interval. We then take the nerve of the clusters.

The full algorithm is given here.

The choice of intervals may drastically affect the resulting complex. For example, consider the two constructions below:

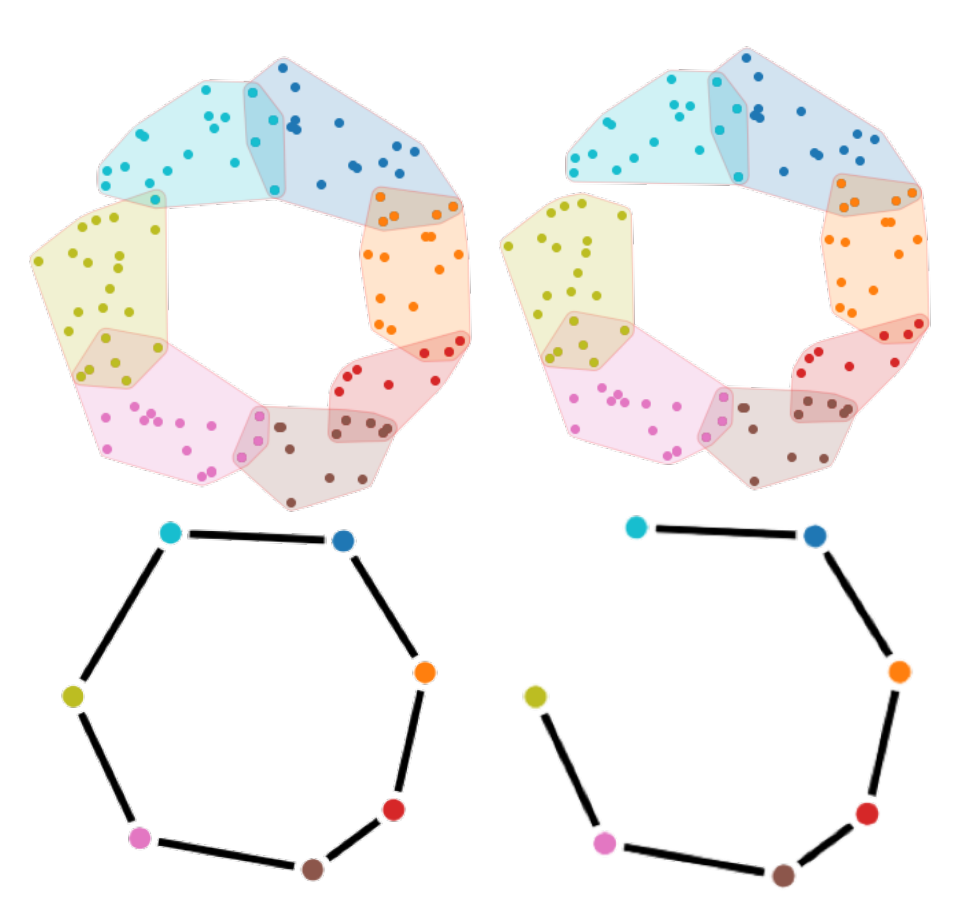
By slightly shrinking an interval, the single point that was in both yellow and cyan regions is now no longer in the yellow region. This results in the yellow-cyan edge in the nerve being removed. From a path perspective, the path from yellow to cyan goes from one edge to six edges.

Cover Filtrations

We construct a filtration given by a distance on covers.

Steinhaus Distance

Given a measure $\mu$, the Steinhaus distance between two sets $A$ and $B$ is

$$d_{St}(A,B)=1-\frac{\mu (A\cap B)}{\mu (A\cup B)}=\frac{\mu (A\cup B)-\mu (A\cap B)}{\mu (A\cup B)}.$$

The Steinhaus distance is bounded on $[0,1]$ and is based on the Jaccard distance. Indeed, since $A\cap B\subseteq A\cup B$, the ratio of measures is between 0 and 1. In a sense, the Steinhaus distance measures “how little” the two sets intersect. When they don’t intersect at all, we get a distance of one. When $A=B$, the distance is zero.

Naturally, this can be extended to a collection of sets:

$${\mu }_{St}(\{U_i\})=1-\frac{\mu (\bigcap U_i)}{\mu (\bigcup U_i)}.$$

When constructing the nerve of our cover, we keep track of the Steinhaus distance.

Steinhaus Nerve

The Steinhaus nerve of a cover $\mathcal{U}$, denoted ${\text{Nrv}}_{St}(\mathcal{U})$, is the nerve of $\mathcal{U}$ where each simplex is assigned a weight given by

$$w_{\sigma }=d_{St}(\{U_i\in \mathcal{U}|i\in \sigma \}).$$

We claim that $w_{\tau }\le w_{\sigma }$ whenever $\tau ⪯\sigma$. Notice that if $\tau ⪯\sigma$ and $\sigma$ is generated from the cover $\{U_i{\}}_{i\in I}$, then $\tau$ must be generated by the subcover $\{U_i{\}}_{i\in J}$, $J\subset I$. Thus, when taking the unions and intersections:

$$\mu \left(\bigcap _{i\in J}{U}_i\right)\ge \mu \left(\bigcap _{i\in I}{U}_i\right)\text{ and }\mu \left(\bigcup _{i\in J}{U}_i\right)\le \mu \left(\bigcup _{i\in I}{U}_i\right).$$

As a result we get the filtration

$$\varnothing =K^{t_0}\subset K^{t_1}\subset K^{t_2}\subseteq \dots$$

where $K^{t_i}:=\{\sigma \in {\text{Nrv}}_{St}(\mathcal{U})\mid w_{\sigma }\le t_i\}$ for $t_i\in [0,1]$.

This construction can have upto $2^{|\mathcal{U}|}-1$ vertices and dimension $|\mathcal{U}|-1$. Computationally, we need to compute the volume of both intersections an unions of sets. If $C_{\text{Unn}}$ and $C_{\text{Int}}$ are the computational cost of computing the volumes of unions and intersections, respectively, then each simplex costs $C_{\text{Unn}}+C_{\text{Int}}$. Resulting in a worst-case scenario of $(C_{\text{Unn}}+C_{\text{Int}})(2^{|\mathcal{U}|}-1)$.

Stability

We focus on stability in terms of changes in the cover.

Bottleneck metric on covers

Let $\mathcal{U}$ and $\mathcal{V}$ be two finite covers of a finite set $X$ such that $|\mathcal{U}|=|\mathcal{V}|$. Let $\mathcal{M}(\mathcal{U},\mathcal{V})$ be the set of all possible matchings. Then the bottleneck distance between two covers is defined as

$$d_B(\mathcal{U},\mathcal{V})=\underset{M\in \mathcal{M}(\mathcal{U},\mathcal{V})}{\min }\left\{\underset{(U,V)\in M}{\max }\mu (U\Delta V)\right\}$$

where $\Delta$ is the symmetric difference.

One may verify that $d_B$ is a metric on the space of finite covers of a finite set.

The following theorem, shows that for two covers of the same size, the Steinhaus nerve are $\alpha /m$ interleaved, i.e.,

$$d_{St}(V_I)-\frac{\alpha }{m}\le d_{St}(U_I)\le d_{St}(V_I)+\frac{\alpha }{m}$$

where $V_I\subset \mathcal{V}$ and $U_I\subset \mathcal{U}$.

Thm

Suppose that $\mathcal{U}=\{U_i\}$ and $\mathcal{V}=\{V_i\}$ are two covers of $X$ with $|\mathcal{U}|=|\mathcal{V}|$ and $d_B(\mathcal{U},\mathcal{V})\le \alpha$. Given $m=\min \{{\min }_{U\in \mathcal{U}}\mu (U),{\min }_{V\in \mathcal{V}}\mu (V)\}$, ${\text{Nrv}}_{St}(\mathcal{U})$ and ${\text{Nrv}}_{St}(\mathcal{V})$ are $\alpha /m$ interleaved filtrations.

The idea of the theorem is the following question: what is the largest change in Steinhaus distance possible between collections $U_I$ and $V_J$?

When $|\mathcal{U}|>|\mathcal{V}|$, then there is some vertex $v\in {\text{Nrv}}_{St}(\mathcal{U})$ not present in ${\text{Nrv}}_{St}(\mathcal{V})$. As a result they cannot be interleaved.

Equivalence

Let ${\text{Cˇ}}_r(X)$ be the cover of $X$ by balls of radius $r$. Then the Cech complex is the nerve of this cover. The Cech filtration is the sequence of complexes given by letting $r\to \infty$.

Conjecture: Given finite $X\subset {\mathbb{R}}^n$ and $R>\text{diam}(X)$, the Cech filtration is isomorphic to the Steinhaus filtration constructed from ${\text{Cˇ}}_R(x)$ under the Lebesgue measure.

The paper starts with proving there is a bijection between $n$-skeletons in the 1-dimensional case. See daily entry 2024-03-29 for details. The bijection is given by

$$C(\{v_i\})=\frac{R{d}_{St}(\{V_i\})}{2-d_{St}(\{V_i\})}$$

where $C(\{v_i\})$ is the Cech birth radius of the simplex defined by vertices $\{v_i\}$ and $\{V_i\}$ is the set of $R$-balls centered at each vertex $\{v_i\}$.

The paper then moves on to the 1-skeleton in any arbitrary dimension. Notice that if the 1-skeletons of the two constructions are isomorphic, then the cover filtration is isomorphic to the Vietoris-Rips filtration since VR is formed by initially finding the 1-skeleton of the Cech complex.

Lemma

The Vietoris-Rips filtration completely determines the cover filtration in arbitrary dimensions.

While the paper doesn’t provide a bijection between the two, they do provide a mapping from the birth time of edges in the Cech filtration to birth time of edges in the cover filtration. More specifically, this map is given by the Steinhaus distance (with Lebesgue measure) of two spheres in ${\mathbb{R}}^n$ with radius $R$ that have a Euclidean distance of $d$:

$$d_{St}^n(R,d)=\frac{2V_{\circ }^n(R)-2_{\cap }^n(R,d)}{2V_{\circ }^n(R)-V_{\cap }^n(R,d)}$$

where $V_{\circ }^n(R)$ is the volume of a hypersphere of radius $R$ and $V_{\cap }^n(R,d)$ is the volume of intersection between two hyperspheres both with radius $R$ whose centers have distance $d$. Both terms involve the gamma function and are messy to compute. The term $V_{\cap }^n(R,d)$ was derived by Li in 2011.

The paper does not demonstrate that this mapping is bijective, and the existence of an inverse is not clear from the map. However, the existence of the map does suggest we can derive the cover filtration from the VR filtration. More precisely, once the VR filtration is constructed, we can construct the cover filtration by evaluating $d_{St}^n(R,d)$ given above for each radius $R$ in the VR filtration.

While the conjecture was not definitely proven, experimental results are given that reinforce the validity of the claim:

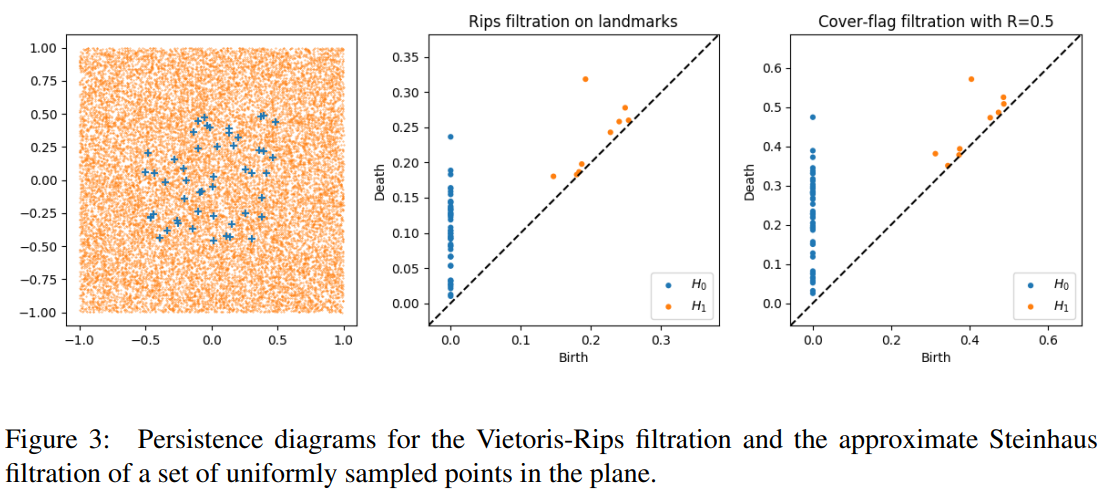
The left most plot shows a uniform data set of 20,000 points with 50 sampled landmark points. The middle plot gives the persistence diagram of dimensions 0 and 1 for the VR filtration. Whereas the right plot gives an approximated persitence diagrams (dimensions 0 and 1) for the Steinhaus filtration based on the landmarks. The selected cover was balls of radii 0.5.

The two persistence diagrams have minimal differences, which is to be expected if the conjecture holds true as the Steinhaus filtration is approximated.

Stable Paths

We want a method to find “stable” paths in the 1-skeleton of a cover filtration. That is, paths with the least distance. That is, the Steinhaus distance. This differs from the shortest path which would be the path with fewest edges.

\rho-Stable path

Given a Steinhaus distance $\rho$, a path $P$ is defined to $\rho$-stable if

$$\max \{d_{St}(e)\mid e\in P\}\le \rho .$$

In other words, a path is $\rho$-stable if each step along the path is at most $\rho$ far. Clearly, if ${\rho }_1\le {\rho }_2$ then a ${\rho }_1$-stable path is also ${\rho }_2$-stable. Moreover, when ${\rho }_1<{\rho }_2$, then we have a higher confidence that a ${\rho }_1$-stable path $P_1$ is not due to noise than a less stable ${\rho }_2$-stable path $P_2$. We want to find the maximally stable paths between two vertices.

Maximally Stable Path

Given a pair of vertices $s$ and $t$, a maximally stable s-t path is a $\rho$-stable path between $s$ and $t$ for the smallest value of $\rho$. In the case of multiple s-t paths with the same minimum $\rho$-value, the shortest of the paths is used.

Finding the maximally stable path is a minimax path problem on undirected graphs. That is, we want to minimize the maximum edge weight. See daily note 2024-04-02 for more details.

There are two paths of relevant: the shortest path, and the most stable. We want to compare the two by computing the Pareto frontier between the two paths:

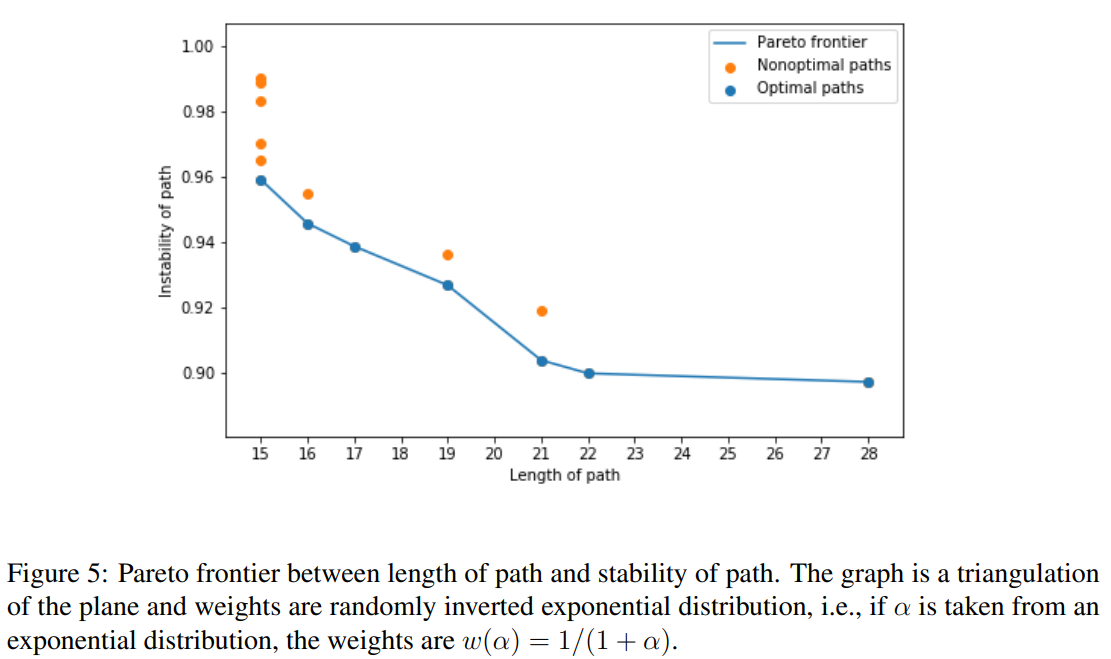
We repeatedly compute the shortest path (orange dots above) while keeping track of the cheapest known path and removing all edges with distance larger than $\rho$.

Input: 1-skeleton G of cover filtration and vertices s,t

set LIST = [] // stores path P and cost p pairs
while s and t are connected in G:
    compute shortest path P between s and t
    set p = max edge distance in P

    if LIST has no path P' where |P|=|P'|:
        add (P,p) to LIST
    else if p < p' for path (P',p') in LIST where |P|=|P'|:
        replace (P',p') with (P,p) in LIST

    remove all edges e from G with distance >= p

Application: Recommendation Systems

Consider the following question: What movies should I show my friend first, to wean them into my favorite movie?