2024-09-06

The following is a brief summary of Persistence stability for geometric complexes.

---

Introduction

Given a data set on a metric space $(Y,d_Y)$ that approximates a metric space $(X,d_X)$, we want to construct a simplicial complex on $Y$ such that $X$ and $Y$ have the same homology or homotopy type. In most applications, $Y$ is finite.

One common approach is to use Vietoris-Rips complex:

$$\sigma =[x_0,x_1,\dots ,x_k]\in \text{Rips}(X,\alpha )\iff d(x_i,x_j)\le \alpha ,\forall i,j=0,1,\dots ,k.$$

For a closed Riemannian manifold $X$, the geometric realization of the Vietoris-Rips complex $\text{Rips}(Y,\alpha )$ that approximates $X$ is homotopy equivalent for sufficiently small $\alpha$. That is, if the Gromov-Hausdorff distance between $X$ and $Y$ is sufficiently small, then there is some $\alpha$ such that $\text{Rips}(Y,\alpha )$ is homotopy equivalent to $X$.

Finding the correct radius $\alpha$ can be difficult in practice. To simplify things we often take the persistence module

$$\text{Rips}(X)=(\text{Rips}(X,\alpha ){)}_{\alpha \in \mathbb{R}}.$$

It was shown by Chazal et. al. that if $X$ and $Y$ are finite metric spaces, then

$$d_b(\text{dgm}(\text{Rips(X)}),\text{dgm}(\text{Rips}(Y)))\le 2d_{GH}(X,Y)$$

where $d_b$ is the bottleneck distance and $d_{GH}$ is the Gromov-Hausdorff distance. This result is beneficial as the bottleneck distance is computationally simpler than the Gromov-Hausdorff distance. Thus, we seek upper bounds on the bottleneck distance.

Thm

If $\mathbb{U}$ is a $q$-tame persistence module then it has a well-defined persistence diagram $\text{dgm}(\mathbb{U})$. If $\mathbb{U}$ and $\mathbb{V}$ are $q$-tame persistence modules that are $ϵ$-interleaved then

$$d_b(\text{dgm}(\mathbb{U}),\text{dgm}(\mathbb{V}))\le ϵ.$$

See 2024-08-30 for more details.

Gromov-Hausdorff Distance

Let $A$ be a closed subset of a metric space $(X,d)$. For $r>0$ we define the $r$-thickening of $A$ to be given by

$$A^{(r)}=\bigcup _{x\in A}B(x,r)$$

where $B(x,r)$ is the ball centered at $x$ with radius $r$. We define the Hausdorff distance by

$$d_H(A,B)=\inf \{r>0:B\subset A^{(r)}\text{ and }A\subset B^{(r)}\}.$$

One may view the Hausdroff distance as the farthest distance from any point of $B$ from $A$, or the farthest distance any point of $A$ from $B$ (take the larger of the two). This distance forms a metric on the set of closed sets in $X$.

The Gromov-Hausdorff distance makes use of the Hausdorff distance to measure the distance between two metric spaces. That is, given two closed metric spaces $A$ and $B$ both inside a larger metric space $X$, the Gromov-Hausdorff distance is given by

$$d_{GH}(A,B)=\underset{f,g}{\inf }{d}_H(f_{A\to X}(A),f_{B\to X}(B))$$

where $f_{A\to X}$ denotes an isometric embedding of $A$ into $X$. We take the infimum over all possible embeddings. The Gromov-Hausdorff distance gives us a measure on how close two metric spaces are from being isometric. As a result, the set of all isometry classes of a metric space is itself a metric space.

One may show that the Gromov-Hausdorff distance is equivalent to the Gromov-Hausdorff approximation which is given by

$$\widehat{d_{GH}}(X,Y)=\underset{f}{\inf }\{ϵ>0:|d_Y(f(x_1),f(x_2))-d_X(x_1,x_2))|<ϵ,\forall x_1,x_2\in X\}.$$

ε-simplicial Multi-valued Maps

We extend the notion of maps to allow for multiple outputs. That is, we define a multi-valued map $C:X\rightrightarrows Y$ to be a subset of $X\times Y$ such that for all $x\in X$, there is some $y\in Y$ such that $(x,y)\in C$, i.e., the projection $(x,y)\mapsto x$ is surjective.

Given two multi-valued maps $C:X\rightrightarrows Y$ and $D:Y\rightrightarrows Z$, we can compose the two to get a new multi-valued map $D\circ C:X\rightrightarrows Z$ where $(x,z)\in D\circ C$ if and only if there is some $y\in Y$ such that $(x,y)\in C$ and $(y,z)\in D$.

We say that a single-valued map $f:X\to Y$ is subordinate to a multi-valued map $C:X\rightrightarrows Y$, denoted $f:X\stackrel{C}{\to }Y$. if $f(x)\in C(x)$ for all $x\in X$.

Let $\mathbb{S}$ and $\mathbb{T}$ be filtered simplicial complexes with vertex sets $X$ and $Y$. We say that a multi-valued map $C:X\rightrightarrows Y$ is $ϵ$-simplicial if for any $\alpha \in \mathbb{R}$ and any simplex $\sigma \in S_{\alpha }$ it follows that every finite subset of the image $C(\sigma )$ is a simplex of $T_{\alpha +ϵ}$.

Example: Consider the filtered simplicial complex $\mathbb{S}:S_1\to S_2\to S_3$ where each complex $S_k$ is the standard $k$-simplex. Consider then the multi-valued map given below:

$$C=\{(v_0,v_0^{\prime }),(v_1,v_1^{\prime }),(v_2,v_2^{\prime }),(v_2,v_3^{\prime })\}.$$

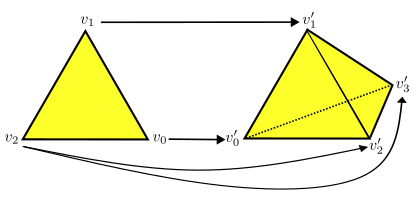
Notice that every simplex $\sigma$ in $S_k$, the subsets of $C(\sigma )$ are simplices in $S_{k+1}$. Therefore, this multi-valued map is 1-simplicial.

$ϵ$-simplicial maps induce a homomorphism of degree $ϵ$ between persistence diagram.

Prp

Given two filtered simplicial complexes $\mathbb{S},\mathbb{T}$ with vertex sets $X,Y$ and a $ϵ$-simplicial map $C:X\rightrightarrows Y$ then $C$ induces the map $H(C)\in {\text{Hom}}^{ϵ}(H(\mathbb{S}),H(\mathbb{T}))$ that is given by $H(f)$ for any $f:X\stackrel{C}{\to }Y$.

Here $H(\mathbb{S})$ is the persistence module we get by applying the simplicial homology functor $S\mapsto H(S)$ to $\mathbb{S}$.

Correspondences

Given a multi-valued map $C:X\rightrightarrows Y$, we say that $C$ is a correspondence if every $y\in Y$ has at least one $x\in X$ such that $(x,y)\in C$, i.e., the projection $(x,y)\mapsto y$ is surjective. Alternatively, one may view a correspondence as a multi-valued map where the transpose $C^{\top }:Y\rightrightarrows X$ given by

$$C^{\top }=\{(y,x)\mid (x,y)\in C\}$$

is also a multi-valued map.

Correspondences can be seen as a form of “weak bijection”. Notice that if $C$ is a correspondence, then

$$1_X=\{(x,x)\mid x\in X\}\subset C^{\top }\circ C\text{ and }{1}_Y=\{(y,y)\mid y\in Y\}\subset C\circ C^{\top }.$$

Moreover if both $C$ and $C^{\top }$ are $ϵ$-simplicial maps, then we get two homomorphisms of degree $ϵ$. It turns out these two homomorphisms induce an $ϵ$-interleaving.

Prp

Let $\mathbb{S},\mathbb{T}$ be filtered simplicial complexes with vertex sets $X$ and $Y$. If $C:X\rightrightarrows Y$ is a correspondence such that $C$ and $C^{\top }$ are both $ϵ$-simplicial, then $H(C)$ and $H(C^{\top })$ induce an $ϵ$-interleaving between $H(\mathbb{S})$ and $H(\mathbb{T})$.

This result applied to $q$-tame persistence modules provides a framework for finding an upper bound on the bottleneck distance, i.e., if two filtered simplicial complexes with $q$-tame persistence modules have a correspondence $C$ between their vertex sets such that $C$ and $C^{\top }$ are $ϵ$-simplicial, then

$$d_b(\text{dgm}(H(\mathbb{S})),\text{dgm}(H(\mathbb{T})))\le ϵ.$$

For example, we claim that given metric spaces $(X,d_X)$ and $(Y,d_Y)$ if $ϵ>2d_{GH}(X,Y)$ then the persistence modules $H(\mathbb{R}\text{ips}(X))$ and $H(\mathbb{R}\text{ips}(Y))$ are $ϵ$-interleaved. To prove this, we first introduce the notion of distortion: given a multi-valued map $C:X\rightrightarrows Y$ between metric spaces, the distortion of $C$ is given by

$$\text{dis}(C)=\sup \{|d_X(x,x^{\prime })-d_Y(y,y^{\prime })|:(x,y),(x^{\prime },y^{\prime })\in C\}.$$

One may show that the Gromov-Hausdorff distance is given by the smallest possible distortion between the two spaces:

$$d_{GH}(X,Y)=\frac{1}{2}\inf \{\text{dis}(C):C:X\rightrightarrows Y\text{ is a correspondence}\}.$$

We may now prove the result.

Lemma

Let $(X,d_X)$ and $(Y,d_Y)$ be metric spaces. If $ϵ>2d_{GH}(X,Y)$ then the persistence modules $H(\mathbb{R}\text{ips}(X))$ and $H(\mathbb{R}\text{ips}(Y))$ are $ϵ$-interleaved.

Proof: Since $ϵ>2d_{GH}(X,Y)$ there is a correspondence $C:X\rightrightarrows Y$ with $\text{dis}(C)\le ϵ$. Take $\sigma \in \text{Rips}(X)$ and a finite subset $\tau \subset C(\sigma )$. Since $\text{dis}(C)\le ϵ$, for any $y,y^{\prime }\in \tau$ there is some $x,x^{\prime }\in \sigma$ such that $y\in C(x)$, $y^{\prime }\in C(x^{\prime })$ and

$$|d_X(x,x^{\prime })-d_Y(y,y^{\prime })|\le ϵ.$$

If we use the reverse triangle inequality then we get that

$$d_Y(y,y^{\prime })\le d_X(x,x^{\prime })+ϵ\le \alpha +ϵ.$$

Therefore, $\tau \in \text{Rips}(Y,\alpha +ϵ)$. Thus, $C$ is $ϵ$-simplicial. A similar argument shows that $C^{\top }$ is also $ϵ$-simplicial. Therefore, the persistence modules $H(\mathbb{R}\text{ips}(X))$ and $H(\mathbb{R}\text{ips})(Y)$ are $ϵ$-interleaved.

Q.E.D.

A similar argument shows this result holds for Cech complexes as well, i.e., the simplicial complex defined by

$$[x_0,x_1,\dots ,x_k]\in \text{Cech}(X,\alpha )\iff \bigcap _{i=0}^{k}B(x_i,\alpha )\ne \varnothing$$

where $B(x_i,\alpha )$ is the closed ball with center $x_i$ and radius $\alpha$.

Lemma

Let $(X,d_X)$ and $(Y,d_Y)$ be metric spaces. If $ϵ>2d_{GH}(X,Y)$ then the persistence modules $H(\mathbb{C}\text{ech}(X))$ and $H(\mathbb{C}\text{ech}(Y))$ are $ϵ$-interleaved.

Stability of Rips and Cech Complexes

We have seen that for sufficiently large $ϵ$ two Rips (or two Cech) persistence modules are $ϵ$-interleaved. We now seek a condition in which they are $q$-tame as well. In such a scenario, we are given an upper bound on their bottleneck distances.

Given a subset $F$ of a metric space $(X,d_X)$, we say that $F$ is an $ϵ$-sample of $X$ if for every $x\in X$, there is some $f\in F$ such that $d_X(x,f)<ϵ$. The metric space is totally bounded if it has a finite $ϵ$-sample for every $ϵ>0$.

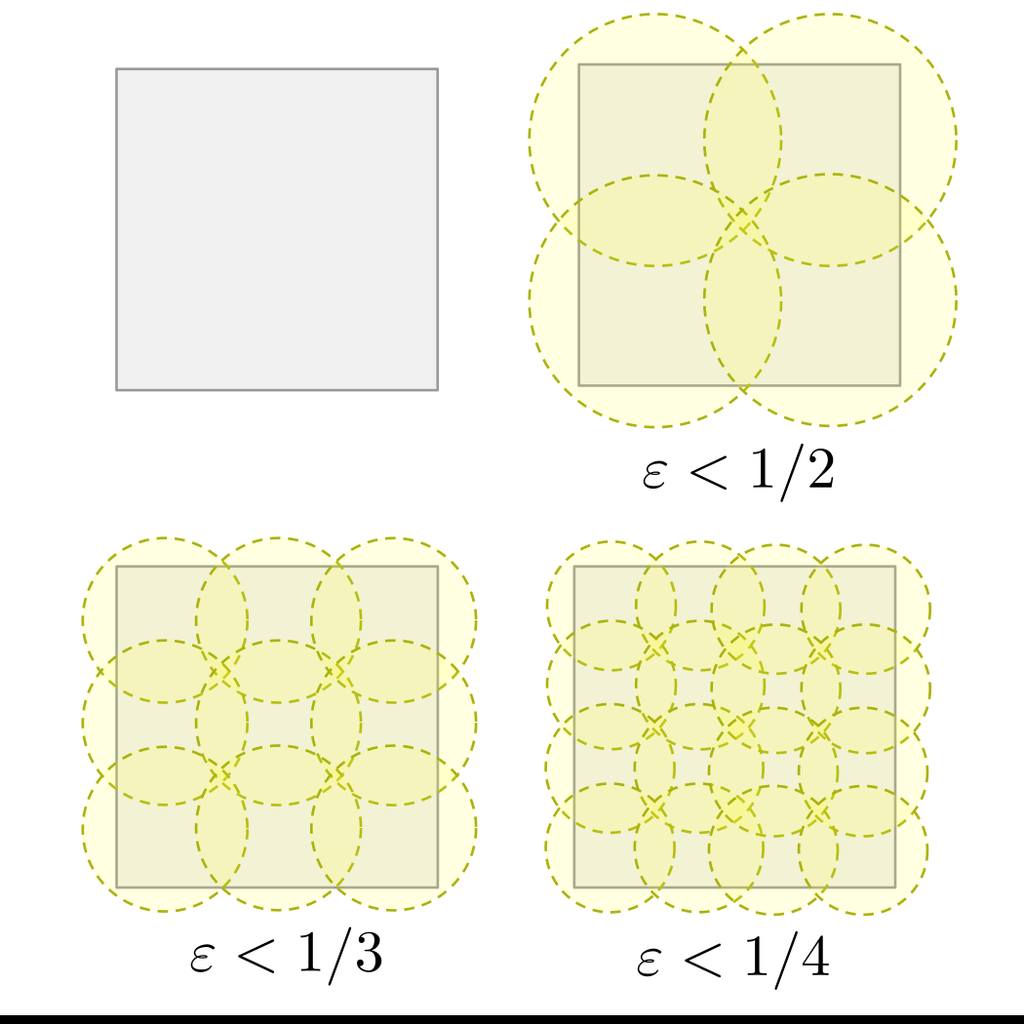
One may alternatively view $ϵ$-samples as subsets that approximate the metric space $X$. Thus, a space is totally bounded if we can approximate $X$ with finitely many points for any level of accuracy $ϵ>0$.

Lemma

If $(X,d_X)$ is totally bounded, then the persistence modules $H(\mathbb{R}\text{ips}(X))$ and $H(\mathbb{C}\text{ech}(X))$ are $q$-tame.

Proof: Let $F$ be an $ϵ/2$-sample and construct the correspondence

$$C=\{(x,f)\in X\times F:d_X(x,f)<\frac{1}{2}ϵ\},$$

i.e., the correspondence that maps every $x\in X$ to its set of approximate values in $F$. Notice that

$$\begin{array}{rl}|d_X(x,x^{\prime })-d_X(f,f^{\prime })|& \le |d_X(x,x^{\prime })-d_X(x,f^{\prime })|+|d_X(x,f^{\prime })-d_X(f,f^{\prime })|\\ & \le d_X(x^{\prime },f^{\prime })+d_X(x,f)\\ & <ϵ.\end{array}$$

Thus, $2d_{GH}(X,F)<ϵ$ which implies that there is an $ϵ$-interleaving between $H(\mathbb{R}\text{ips}(X))$ and $H(\mathbb{R}\text{ips}(F))$. Notice that for $ϵ=(b-a)/2$ the map $I_a^b:\text{Rips}(X,a)\to \text{Rips}(X,b)$ factors into

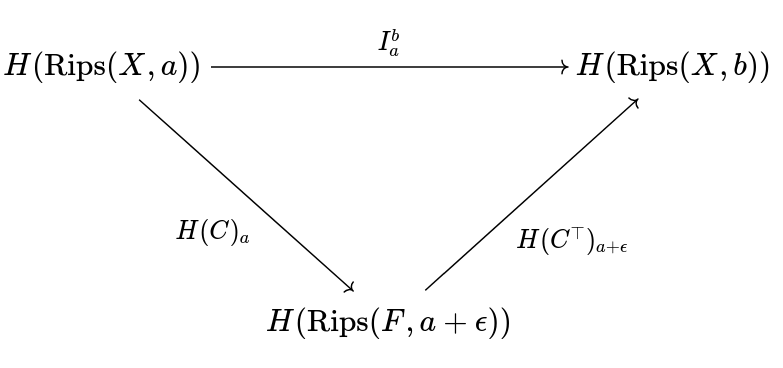
Since $F$ is finite dimensional, $H(\text{Rips}(F,a+ϵ))$ is finite-dimensional. Therefore, $I_a^b$ has finite rank, i.e., the persistence module is $q$-tame. The proof for the Cech complex is the same.

Q.E.D.

As a consequence, we get an upper bound on the bottleneck distances.

Thm

Let $X$ and $Y$ be totally bounded metric spaces. Then

$$d_b(\text{dgm}(H(\mathbb{R}\text{ips}(X))),\text{dgm}(H(\mathbb{R}\text{ips}(Y))))\le 2d_{GH}(X,Y)$$

and

$$d_b(\text{dgm}(H(\mathbb{C}\text{ech}(X))),\text{dgm}(H(\mathbb{C}\text{ech}(Y))))\le 2d_{GH}(X,Y).$$

Note that there exists simplicial complexes $X$ such that $H(\mathbb{R}\text{ips}(X))$ is not $q$-tame. For example, define

$$X=\{(t,0)\in {\mathbb{R}}^2:t\in [0,1]\}\cup \{(t,1)\in {\mathbb{R}}^2:t\in [0,1]\}.$$

Notice that for any $t\in [0,1]$ the edge $e_t=[(t,0),(t,1)]$ is in $\text{Rips}(X,1)$ but is not on the boundary of a triangle. Thus, for each $t\in [0,1]$ the cycles

$${\gamma }_t=[(0,0),(t,0)]+[(t,0),(t,1)]-[(0,1),(t,1)]-[(t,0),(t,1)]$$

form a linearly independent set in $H_1(\text{Rips}(X,1))$, i.e., the first homology group corresponding to a radius of 1 has an uncountable dimension.