2025-06-26

Meeting Summary: Amber, Bala, & Bei

We are interested in either extending or generalizing current work on contour boxplots. Current approaches make use of a notion of depth of a data point. For instance in $\mathbb{R}$, consider the points $v_1<v_2<\cdots <v_5$. The data point $v_4$ would have $\text{depth}(v_4)=3$ as it is contained in 3 intervals ($(v_1,v_5)$, $(v_2,v_5)$, and $(v_3,v_5)$) where as $\text{depth}(v_3)=4$ as it is contained in 4 intervals. One may view $\text{depth}(\cdot )$ as a measure of centrality. Hence, we can view the median entry as the entry of maximal depth.

We would like to use this notion of depth in the case of a data set consisting of curves. However, identifying containment of a curve between two other curves is less clear as we see in the example below:

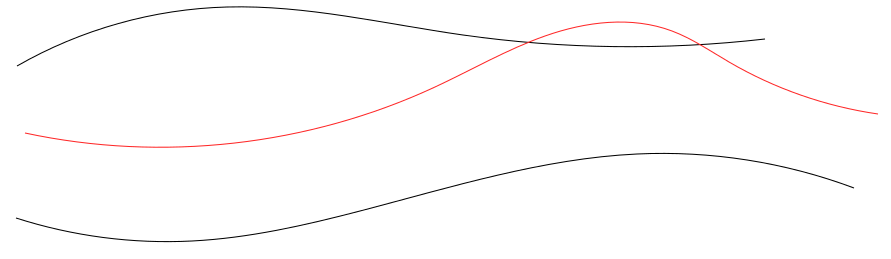
The red curve above doesn’t lie between the two curves, but most of the curve does. Perhaps we could modify the definition of depth to include some error parameter $ϵ$ where we consider a curve $\gamma$ being nested between two other curves ${\gamma }_1$ and ${\gamma }_2$ if it lies between them for all but some area $\mu \le ϵ$. This leads to the following question:

Main Question: Can we apply flat norm curve simplification to contour boxplots?

Doing any sort of flat norm operation on the curves leaves us with two potential versions:

1. Simplify curves ${\gamma }_1$ and ${\gamma }_2$ to form $\widehat{{\gamma }_1}$ and $\widehat{{\gamma }_2}$ and use the new curves to check if $\gamma$ is nested between $\widehat{{\gamma }_1}$ and $\widehat{{\gamma }_2}$.
2. Transform input $\gamma \mapsto \hat{\gamma }$ such that $\hat{\gamma }$ is nested between ${\gamma }_1$ and ${\gamma }_2$.

We can also view the second version as finding the minimal amount of perturbation $ϵ$ to “untangle” the input curve. This also would allow us to change from a single true/false binary in our $\text{nested}$ check to a continuous weight. Where a smaller $ϵ$ is given a higher weight (perhaps something like $1/ϵ$). From here we could define the depth of a curve $\gamma \in \Sigma$ by the sum

$$\sum _{({\gamma }_1,{\gamma }_2)\in \Sigma \times \Sigma }\text{nested}(\gamma ,{\gamma }_1,{\gamma }_2).$$