Finding the Homology of Submanifolds with High Confidence from Random Samples

Questions:

• Condition number $1/\tau$ of a manifold $\mathcal{M}$
• Their definition of the orientation of the faces in ${\partial }_j\sigma$ varies from class (no concern on parity of index)

Full paper can be found at: https://link.springer.com/article/10.1007/s00454-008-9053-2

Introduction

The class of problems known as manifold learning attempts to estimate the geometrical and topological properties of a submanifold from random points lying on said unknown manifold. The paper provides an algorithm to identify the homology of the submanifold using only random samples. The algorithm works well with noise where the points lie near the submanifold rather than on it.

Preliminaries

Let $M$ be a topological space. A chart $(U,\phi )$ on $M$ consists of an open set $U\subset M$ and homeomorphism $\phi :U\to {\mathbb{R}}^d$ such that $\phi (U)$ is open. Given two overlapping charts $(U_{\alpha },{\phi }_{\alpha })$ and $(U_{\beta },{\phi }_{\beta })$ we construct a transition map ${\phi }_{\alpha }\circ {\phi }_{\beta }^{-1}:{\phi }_{\alpha }(U_{\alpha }\cap U_{\beta })\to {\phi }_{\beta }(U_{\alpha }\cap U_{\beta })$ which allows one to “smoothly” transition between charts.

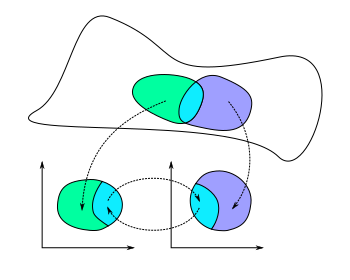
We call a topological space $M$ a smooth manifold if it has a collection of charts $\{(U_{\alpha },{\phi }_{\alpha })\mid \alpha \in A\}$ such that each $\{U_{\alpha }{\}}_{\alpha \in A}$ covers $M$ and for all $\alpha ,\beta \in A$ the transition map ${\phi }_{\alpha }\circ {\phi }_{\beta }^{-1}$ is $C^{\infty }$.

For every point $p\in M$ on a smooth manifold, there is an associated tangent space $T_{p}M$ consisting of vectors tangent to $M$ at the point $p$. A Riemannian metric $g$ on $M$ assigns a positive-definite inner product $g_p:T_{p}M\times T_{p}M\to \mathbb{R}$. A smooth manifold with a Riemannian metric is called a Riemannian manifold. In summary, a Riemannian manifold is a smooth manifold with a notion of distance, angles, length and curvature.

Given a compact Riemannian manifold $\mathcal{M}\subset {\mathbb{R}}^N$, we define the set

$$G=\{x\in {\mathbb{R}}^N\mid \exists \text{ distinct }p,q\in \mathcal{M}\text{ where }d(x,\mathcal{M})=\Vert x-p\Vert =\Vert x-q\Vert \},$$

where $d(x,\mathcal{M})={\inf }_{y\in \mathcal{M}}\Vert x-y\Vert$ is the distance of $x$ to $\mathcal{M}$. The closure of $G$ forms the medial axis and for any $p\in \mathcal{M}$ the local feature size $\sigma (p)$ is the distance of $p$ to the medial axis. We define the condition number of $\mathcal{M}$ to be $1/\tau$ where

$$\tau =\underset{p\in \mathcal{M}}{\inf }\sigma (p).$$

For example, if $\mathcal{M}$ is a sphere of radius $r$, then the medial axis is the sphere’s center point and $\tau =r$.

Main Results

We wish to compute the homology of a manifold $\mathcal{M}\subset {\mathbb{R}}^N$ from the randomly sampled data points $\overline{x}=\{x_1,\dots ,x_n\}\subset \mathcal{M}$. To reconstruct the manifold from $\overline{x}$ we construct open Euclidean balls $B_{ϵ}(x_i)$ with radius $ϵ$ centered at each $x_i\in \overline{x}$. We then define

$$U=\bigcup _{x\in \overline{x}}{B}_{ϵ}(x)$$

to be the reconstructed manifold.

Proposition 3.1

Let $\overline{x}$ be any finite collection of points $x_1,\dots ,x_n\in {\mathbb{R}}^N$ such that for every $p\in \mathcal{M}$, there exists an $x\in \overline{x}$ such that $\Vert p-x{\Vert }_{{\mathbb{R}}^N}<ϵ/2$. Then for any $ϵ<\sqrt{3/5}\tau$ we have that $U$ deformation retracts to $\mathcal{M}$. Therefore the homology of $U$ equals the homology of $\mathcal{M}$.

For example, consider a circle. If for every $p\in \mathcal{M}$ there is a point $x_i\in \overline{x}$ such that $\Vert p-x_i{\Vert }_{{\mathbb{R}}^2}<ϵ/2$, then the union of balls $U$ deformation retracts to $\mathcal{M}$ as long as $ϵ<\sqrt{3/5}\tau$.

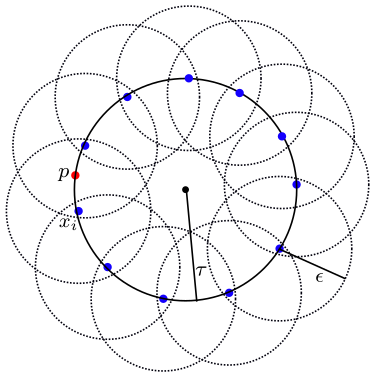
The question then is what the probability that points $x_1,\dots ,x_n$ sampled in an i.i.d. fashion (independent and identically distributed) satisfy the above. \

Proposition 3.2

Let $\overline{x}$ be drawn by sampling $\mathcal{M}$ in i.i.d. fashion according to the uniform probability measure on $\mathcal{M}$. Then with probability greater than $1-\delta$ we have that $\overline{x}$ is $(ϵ/2)$-dense ($ϵ<\tau /2)$ in $\mathcal{M}$ provided that

$$|\overline{x}|>{\beta }_1\left(\log ({\beta }_2)+\log \left(\frac{1}{\delta }\right)\right)$$

where

$${\beta }_1=\frac{\text{vol}(\mathcal{M})}{({\cos }^k({\theta }_1))\text{vol}(B_{ϵ/4}^k)}\text{ and }{\beta }_2=\frac{\text{vol}(\mathcal{M})}{({\cos }^k({\theta }_2))\text{vol}(B_{ϵ/8}^k)}.$$

Here $k$ is the dimension of $\mathcal{M}$ and $\text{vol}(B_{ϵ}^k)$ denotes the $k$-dimensional volume of the standard $k$-dimensional ball of radius $ϵ$. Finally, ${\theta }_1=\arcsin (ϵ/8\tau )$ and ${\theta }_2=\arcsin (ϵ/16\tau )$.

Combining Propositions 3.1 and 3.2 provides a way of estimating the probability that the ball reconstruction of the manifold of $n$ i.i.d sampled points has the same homology.

Computing the Homology of $U$

The paper outlines an algorithm for computing the homology of $U$ making use of the nerve of the cover $U={\bigcup }_{x_i\in \overline{x}}{B}_{ϵ}(x_i)$.

1. Define $L_j$ to be the collection of all $j$-simplices in the nerve of $U$, i.e., each $\sigma \in L_j$ is associated with $j+1$ points $(p_0(\sigma ),\dots ,p_j(\sigma )\in \overline{x})$ such that

$$\bigcap _{i=0}^j{B}_{ϵ}(p_i(\sigma ))\ne \varnothing$$

2. The size $|L_j|$ is bounded above by $\left(\genfrac{}{}{0ex}{}{n}{j+1}\right)$. However, the actual size is much smaller as two points $x_m$ and $x_n$ more than $2ϵ$ apart are not associated to a simplex. Define the simplicial complexes $K_j={\bigcup }_{i=0}^j{L}_j$ with face relations, then the nerve of $U$ is $K=K_N$.
3. We can compute the simplicial complex by the following decision problem: for any set of $j$ points, determine whether balls of radius $ϵ$ around each point have non-empty intersection. It follow that ${\bigcap }_{i=1}^j{B}_{ϵ}(p_i)\ne \varnothing$ if and only if the smallest radius enclosing all the points is less than $ϵ$.
4. We define a $j$-chain to be a function $c:L_j\to \mathbb{R}$, which is written as formal sum

$$c=\sum _{\sigma \in L_j}c(\sigma )\sigma .$$

Adding $j$-chains componentwise forms a vector space of $j$-chains denoted by $C_j$.

5. The boundary operator ${\partial }_j:C_j\to C_{j-1}$ is defined as follows: for each (oriented) simplex $\sigma \in L_j$,

$${\partial }_j\sigma =\sum _{i=0}^j(-1{)}^i{\sigma }_i,$$

where ${\sigma }_i$ is a $j-1$ face of $\sigma$ and the orientation of ${\sigma }_i$ is given by $|p_0,\dots ,p_{i-1},p_{i+1},\dots ,p_j|$. Thus, ${\partial }_j$ is then defined on $j$-chains by additivity by

$${\partial }_j\left(\sum _{\sigma \in L_j}c(\sigma )\sigma \right)=\sum _{\sigma \in L_j}c(\sigma ){\partial }_j\sigma$$

One may view ${\partial }_j$ as an $n_{j-1}\times n_j$ matrix where $n_i=|L_i|$.

6. The boundary operator forms a chain complex

$$\cdots \to C_{j+1}\stackrel{{\partial }_{j+1}}{\to }{C}_j\stackrel{{\partial }_j}{\to }{C}_{j-1}\to \cdots$$

We define the $j$-th homology group as the vector space quotient

$$H_j=\text{Ker}{\partial }_j/\text{Im}{\partial }_{j+1}$$

where

$$\text{Ker}{\partial }_j=\{c\in C_j\mid {\partial }_{j}c=0\}$$

and

$$\text{Im}{\partial }_j=\{c\in C_{j-1}\mid \exists c^{\prime }\in C_j\text{ where }{\partial }_j{c}^{\prime }=c\}.$$

The Deformation Retract Argument