Witness Complex

Let $\sigma =[v_0\dots v_k]$ be a $k$-simplex with vertices in $v_i\in S\subset {\mathbb{R}}^d$. We say $x\in {\mathbb{R}}^d$ is a weak witness for $\sigma$ with respect to $S$ if

$$\Vert x-v\Vert \le \Vert x-u\Vert \forall v\in \{v_0,\dots ,v_k\},u\in S\backslash \{v_0,\dots ,v_k\}.$$

A weak witness is a strong witness if

$$\Vert x-v_0\Vert =\Vert x-v_1\Vert =\cdots =\Vert x-v_k\Vert .$$

For example, in the Delaunay complex below

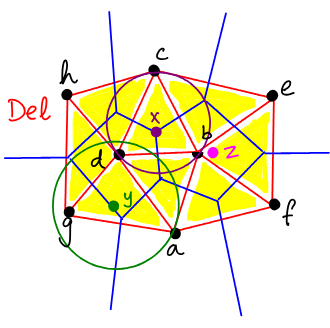
$x$ is a strong witness for $\Delta bcd$ since each vertex is equidistant to $x$. The point $y$ is a weak witness for $\overline{dg}$ and $\Delta adg$. As drawn,

$$\Vert y-g\Vert <\Vert y-d\Vert <\Vert y-a\Vert <\Vert y-v\Vert \text{ for }v=b,c,e,f,h.$$

One may notice that every triangle in ${\text{Del}}_S$ has a strong witness at the center of the triangles circumcircle.

de Silva, 2003

A simplex $\sigma \subset S$ has a strong witness if and only if every face $\tau ⪯\sigma$ has a weak witness.

The witness complex is all simplices that have a weak witness.

Witness Complex

The (strict) witness complex $W_{\infty }(L,S)$ is the collection of simplices $\sigma \subset L$ that have a weak witness in $S$.

Relationship to Delaunay

One may see that a simplex $\sigma \in {\text{Del}}_L$ if and only if $\sigma$ has a strong witness. But if $\sigma \in W_{\infty }(L,S)$, then all faces have a weak witness implying by Theorem 1 that $\sigma$ has a strong witness. As a result,

$$W_{\infty }(L,S)\subseteq {\text{Del}}_L.$$

Computationally we often use the lazy witness complex, which similar to the Vietrois-Rips complex we find the 1-skeleton then fill in holes.

Lazy Witness Complex

The lazy witness complex $W_1(L,S)\supset W_{\infty }(L,S)$ is given by constructing the 1-skeleton of $W_{\infty }(L,W)$ then adding $\sigma =[v_0\dots v_k]$ if and only if each edge $\tau \prec \sigma$ is in $W_1(L,S)$.

Choosing Landmarks

Before choosing landmarks, we need to determine $|L|$. According to de Silva and Carlsoon (2004) if $S$ is sampled from surfaces in 3D then $|L|\le \frac{n}{20}$ is a good upper bound.

Once you’ve determined the number of landmarks, there are two common methods.

1. Random selection of points in $S$
2. Maxmin selection

Maxmin selection works by first picking the first landmark ${\ell }_1$ randomly. Then inductively, we choose the next landmark ${\ell }_i$ which maximizes the function

$$z\mapsto \max \{d(z,{\ell }_1),\dots ,d(z,{\ell }_{i-1}\}.$$

As a result, we get a widespread coverage of $S$ with the downside that we may end up with outliers as landmarks.