2024-10-10

The $q$-tame example from 2024-10-08 is still not quite right. While the first homology group does have infinite dimension, the problematic map in question goes from the trivial group. Thus, the image of the map will be trivial, hence finite rank. We can tweak the problem by making half the diamonds be born at a different point in time. This can be done simply by tweaking the size of half the blue boxes.

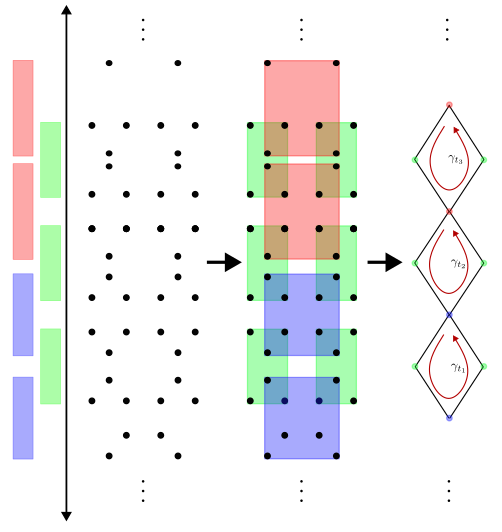
The center boxes have the pattern: blue, blue, red, red, blue, blue, red, red, etc.

Now the sizes of the boxes are as follows:

$$\begin{array}{rl}R& =11\times 14\\ G& =6\times 11\\ B& =11\times 12\\ R\cap G& =2.5\times 4\\ B\cap G& =2.5\times 3.\end{array}$$

This gives two different Steinhaus distances:

$$1-\frac{\mu (B\cap G)}{\mu (B\cup G)}=1-\frac{7.5}{6\times 11+11\times 12-7.5}=\frac{366}{381}\approx 0.961$$

and

$$1-\frac{\mu (R\cap G)}{\mu (R\cup G)}=1-\frac{10}{11\times 14+6\times 11-10}=\frac{200}{210}\approx \mathrm{0.952.}$$

Thus, the cycles going around the red-green-red-green diamonds in the complex are born at time $200/210$ before the remaining diamonds are born at time $366/381$. Therefore, in the first homology persistence module, the map from $200/210$ to $370/383$ has infinite rank.