Currents and the Flat Norm

The Wedge Product and Multivectors

Let $V$ be a vector space. The wedge product is a multilinear alternating operation, i.e.,

$$\begin{array}{rl}c{v}_1\wedge v_2& =v_1\wedge c{v}_2=c(v_1\wedge v_2)\\ (v_1+v_2)\wedge v_3& =v_1\wedge v_3+v_2\wedge v_3\\ v_1\wedge v_2& =-v_2\wedge v_1.\end{array}$$

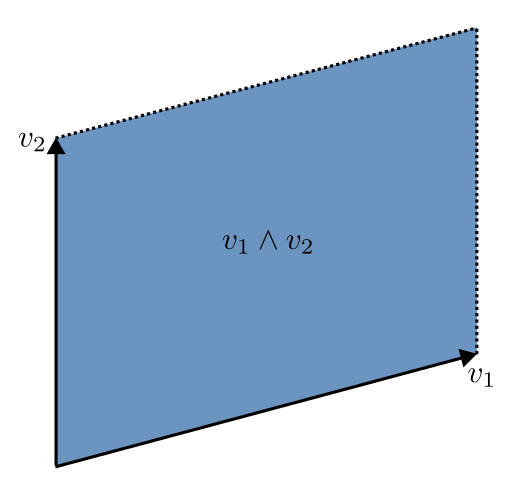
The wedge product was introduced to study the volume of surfaces. For example, let $v=a{e}_1+b{v}_2$ and $w=c{e}_1+d{e}_2$ be vectors in ${\mathbb{R}}^2$. Then the wedge product is

$$\begin{array}{rl}v\wedge w& =(a{e}_1+b{e}_2)\wedge (c{e}_1+d{e}_2)\\ & =ac{e}_1\wedge e_1+ad{e}_1\wedge e_2+bc{e}_2\wedge e_1+bd{e}_2\wedge e2\\ & =(ad-bc)e_1\wedge e_2.\end{array}$$

Notice that $ad-bc$ is the signed area of the parallelogram formed by $v$ and $w$:

$$\det \left[\begin{array}{cc}v& w\end{array}\right]=\det \left[\begin{array}{cc}a& c\\ b& d\end{array}\right]=ad-bc.$$

The signed area has the same magnitude as the area, but is positive or negative depending on the orientation of the surface.

Given three vectors $u,v,w\in {\mathbb{R}}^3$. The scalar coefficient of $u\wedge v\wedge w$ gives the triple product, i.e., the signed volume of the parallelepiped formed by the vectors.

Multivector

Given $m$ vectors $v_1,v_2,\dots ,v_m$ the $m$-vector $\xi$ is given by $\xi =v_1\wedge v_2\wedge \cdots \wedge v_m.$ The vector space of all $m$-vectors is denoted ${\Lambda }_{m}V$.

More generally, if $e_1,\dots ,e_n$ form a basis for $V$, then

$$\xi =\sum _{i_1<\cdots <i_m}{a}_{i_1\cdots i_m}{e}_{i_1}\wedge e_{i_2}\wedge \cdots \wedge e_{i_m}$$

where the sum is taken over all combinations of indices $i_1<\cdots <i_m$ from $1,\dots ,n$. If $m=n$, then

$$v_1\wedge \cdots \wedge v_n=\det \left[\begin{array}{ccc}{v}_1& \cdots & v_n\end{array}\right]e_1\wedge \cdots \wedge e_n.$$

One may view an $m$-vector $\xi =v_1\wedge \cdots \wedge v_m$ as the $m$-dimensional parallelogram formed by the vectors $v_1,\dots ,v_m$ with $m$-dimensional volume given by the magnitude.

Differential Forms

Let $V^{\vee }$ denote the space of covectors dual to $V$, i.e., the set of linear functionals $f:V\to \mathbb{R}$. We often denote the dual orthonormal basis $e_1^{\ast },\dots ,e_n^{\ast }$ by $d{x}_1,\dots ,d{x}_n$, which is given by the linear functional defined by

$$d{x}_i(e_j)=\{\begin{array}{ll}1& i=j\\ 0& i\ne j.\end{array}$$

0-form

A differentiable 0-form is a differentiable function $f:V\to \mathbb{R}$.

1-form

A differential one-form $\alpha$ on $V$ is a covector field, i.e., a map $\alpha :V\to V^{\vee }$ which assigns a covector to each vector.

One may view a one-form as the linear combination

$$\alpha (x)=f_1(x)d{x}_1+f_2(x)d{x}_2+\cdots +f_n(x)d{x}_n.$$

Note that $\alpha$ here can be viewed as a family of linear functionals. That is, given a vector $⟨a,b,c⟩$,

$$(fdx+gdy+hdz)(a,b,c)=f(x_0,y_0,z_0)a+g(x_0,y_0,z_0)b+h(x_0,y_0,z_0)c$$

at the point $(x_0,y_0,z_0)\in V$.

For example, the change in angle form $d\theta$ in ${\mathbb{R}}^2$ is the one-form

$$d\theta =-\frac{y}{x^2+y^2}dx+\frac{x}{x^2+y^2}dy.$$

Integrating over the unit circle $C$ gives

$$\begin{array}{rl}{\int }_{C}d\theta & ={\int }_0^{2\pi }\left(-\frac{y}{x^2+y^2}\frac{dx}{dt}+\frac{x}{x^2+y^2}\frac{dy}{dt}\right)dt\\ & ={\int }_0^{2\pi }\left({\sin }^{2}t+{\cos }^{2}t\right)dt\\ & =2\pi .\end{array}$$

Note that $d\theta$ is simply the gradient $\nabla \theta =⟨{\partial }_x\text{atan2},{\partial }_y\text{atan2}⟩$ viewed as a 1-form.

Visualizing 1-forms

Let $S$ be the 2-sphere in ${\mathbb{R}}^3$. At any point $p\in S$ the sphere has a tangent plane which we denote by $T_{p}S$. This tangent space forms a vector space. The collection of all tangent spaces,

$$TS=\underset{p\in S}{⨆}{T}_{p}S=\{(p,v)\mid p\in S,v\in T_{p}S\},$$

is called the tangent bundle. Taking the dual gives the cotangent bundle, $T{S}^{\ast }$, where now we are assigning each point $p\in S$ a linear functional $v^{\ast }:T_{p}S\to \mathbb{R}$. Under this view, a 1-form is the map $\alpha :S\to T{S}^{\ast }$.

Now let $\phi :\mathbb{R}\to S$ be a curve on the sphere and $\alpha (p)=f(p)dx+g(p)dy$ a 1-form. Then for time $t$ we get a linear functional

$$\alpha (\phi (t))=f(\phi (t))dx+g(\phi (t))dy$$

which eats a vector $v\in T_{\phi (t)}S$ and spits out a number.

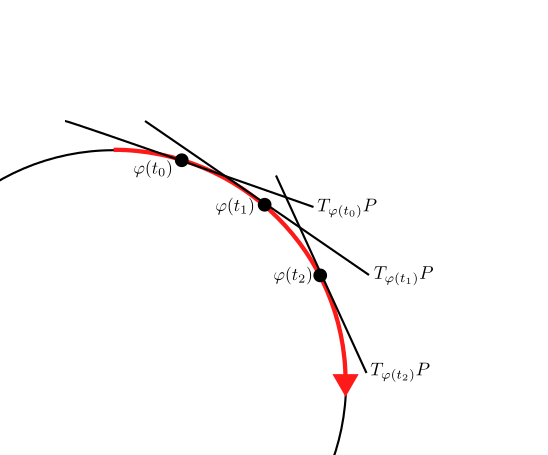
Integrating along $\phi$

m-forms

An $m$-covector is a linear combination of wedge products of covectors, i.e., an $m$-covector is an $m$-vector over the vector space $V^{\vee }$. We denote the space of $m$-covectors by ${\Lambda }^{m}V$.

Differential Form

A differential $m$-form $\omega$ on $V$ is an $m$-covector field, i.e., a map $\omega :V\to {\Lambda }^{m}V$ which assigns a $m$-covector to each vector.

For example, $f(x)dx$ is an example of a 1-form while

$$\omega (x,y,z)=f(x,y,z)dx\wedge dy+g(x,y,z)dz\wedge dx+h(x,y,z)dy\wedge dz$$

is an example of a 2-form.

Exterior Derivative

Given a differential $m$-form

$$\omega =\sum _{i_1<\cdots <i_m}{f}_{i_1\cdots i_m}d{x}_{i_1}\wedge \cdots \wedge d{x}_{i_m}$$

the exterior derivative is the $(m+1)$-form given by

$$d\omega =\sum _{i_1<\cdots <i_m}d{f}_{i_1\cdots i_m}\wedge d{x}_{i_1}\wedge \cdots \wedge d{x}_{i_m}$$

where

$$df=\frac{\partial f}{\partial x_1}d{x}_1+\cdots +\frac{\partial f}{\partial x_n}d{x}_n.$$

For example,

$$\begin{array}{rl}d(fdy\wedge dz+gdz\wedge dx+hdx\wedge dy)& =df\wedge dy\wedge dz+dg\wedge dz\wedge dx+dh\wedge dx\wedge dy\\ & =\frac{\partial f}{\partial x}dx\wedge dy\wedge dz+\frac{\partial f}{\partial y}dy\wedge dy\wedge dz+\frac{\partial f}{\partial z}dz\wedge dy\wedge dz\\ & +\frac{\partial g}{\partial x}dx\wedge dz\wedge dx+\frac{\partial g}{\partial y}dy\wedge dz\wedge dx+\frac{\partial g}{\partial z}dz\wedge dz\wedge dx\\ & +\frac{\partial h}{\partial x}dx\wedge dx\wedge dy+\frac{\partial h}{\partial y}dy\wedge dx\wedge dy+\frac{\partial h}{\partial z}dz\wedge dx\wedge dy\\ & =\left(\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}+\frac{\partial h}{\partial z}\right)dx\wedge dy\wedge dz\end{array}$$

Integration

Differential forms were introduced to allow for integration over manifolds. For example, if $U\subset {\mathbb{R}}^n$ and $\omega =f(x)d{x}_1\wedge \cdots \wedge d{x}_n$ is a $n$-form, then

$${\int }_U\omega :={\int }_{U}f(x)d{x}_{1}d{x}_2\cdots d{x}_n.$$

Currents

Let ${\Omega }_c^m({\mathbb{R}}^n)$ denote the space of smooth $m$-forms with compact support on ${\mathbb{R}}^n$, i.e., $\omega \in {\Omega }_c^m({\mathbb{R}}^n)$ if $C^{\infty }$ and the closure of

$$\{x\in {\mathbb{R}}^n\mid \omega (x)\ne 0\}$$

is compact. A current is an element of the dual space, i.e., it is a linear functional

$$T:{\Omega }_c^m({\mathbb{R}}^n)\to \mathbb{R}$$

that is continuous. One may view them as a generalization of oriented surfaces.

Given a compact rectifiable oriented submanifold $M$ of dimension $m$, one may construct an $m$-current $R$ given by

$$R(\omega )={\int }_M\omega ,$$

i.e., the linear functional that simply integrates the $m$-form over $M$. If the boundary $\partial M$ is rectifiable, then it follows by Stokes’ theorem that

$$\partial R(\omega )={\int }_{\partial M}\omega ={\int }_{M}d\omega =R(d\omega ).$$

Given a $p$-current $T$, it’s boundary $\partial T$ is the $(p-1)$-current that satisfies

$$\partial T(\omega )=T(dw)$$

for all $p$-forms $\omega$. Note that $d(d\omega )=0$, so $\partial (\partial T)=0$.

The space of $m$-currents on ${\mathbb{R}}^n$, denoted ${\mathcal{E}}_m$, defines a real vector space where

$$(T+S)(\omega ):=T(\omega )+S(\omega )\text{ and }(\lambda T)(\omega ):=\lambda T(\omega ).$$

The Flat Norm

Given a current $T:{\Omega }_c^m({\mathbb{R}}^n)\to \mathbb{R}$, the mass of $T$ is given by

$$M(T)=\sup \{T(\omega ):\underset{x}{\sup }\Vert \omega (x)\Vert \le 1\}$$

where

$$\Vert \omega (x)\Vert :=\sup \{|⟨\omega ,\xi ⟩|:\xi \text{ is a unit simple m-vector}\}.$$

The mass of a current can be thought of as the weighted $m$-dimensional volume of the object represented by $T$.

The Flat Norm

Given an $m$-current $T\in {\mathcal{E}}_m$, the flat norm is given by $F(T)=\inf \{M(T-\partial S)+M(S):S\in {\mathcal{E}}_{m+1}\}.$

In summary the flat norm looks at all decompositions of an $m$-current $T$ as $T=(T-\partial S)+S$ for $(m+1)$-currents $S$ and takes the decomposition with smallest sum of masses.