Flow Decomposition

Recall that an arc flow of a network is a vector $x=\{x_{ij}\}$ that satisfies the constraint

$$\sum _{(i,j)\in A}{x}_{ij}-\sum _{(j,i)\in A}=-e(i)\forall i\in N$$

with $0\le x_{ij}\le u_{ij}$ for all $(i,j)\in A$ and

$$\sum _{i\in N}e(i)=0.$$

Note, here we have replaced the supply/node $b(i)$ with $-e(i)$ which represents the imbalance. One may view $e(i)$ as the inflow minus the outflow of node $i$. If $e(i)>0$ then $i$ is an excess node. If $e(i)<0$ then $i$ is a deficit node. Otherwise, inflow and outflow are equal and $i$ is a balanced node.

In flow decomposition we go from flows on arcs to defining flows on paths and cycles. For example, consider the figure below:

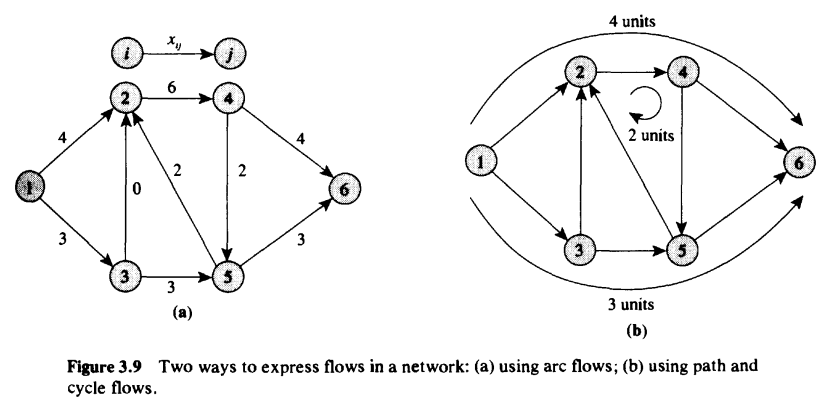
We have decomposed the flow $x_{ij}$ into the paths $P_1=1-2-4-6$, $P_2=1-3-5-6$ and cycle $W=2-4-5-2$. $P_1$ sends 4 units of flow, $P_2$ sends 3 units of flow and cycle $C$ has $2$ units of flow circulating.

If we denote the flow of a path/cycle by $f(P)$, then the set of paths $\mathcal{P}$ and the set of cycles $\mathcal{W}$ in the flow decomposition uniquely determine the flow $x_{ij}$. That is,

$$x_{ij}=\sum _{P\in \mathcal{P}}{\delta }_{ij}(P)f(P)+\sum _{W\in \mathcal{W}}{\delta }_{ij}(W)f(W)$$

where ${\delta }_{ij}(P)$ is the indicator function

$${\delta }_{ij}(P)=\{\begin{array}{ll}1& \text{if arc (i,j)∈P}\\ 0& \text{otherwise.}\end{array}$$

Flow Decomposition Theorem

Every path and cycle flow has a unique representation as nonnegative arc flows. Conversely, every nonnegative arc flow $x$ can be represented as a path and cycle flow (though not necessarily unique) with the following two properties:

1. Every directed path with positive flow connects a deficit node to an excess node.
2. At most $n+m$ paths and cycles have nonzero flow; out of these, at most $m$ cycles have nonzero flow.

Flow Decomposition Algorithm

Define the following:

$$\begin{array}{rl}y& :\text{intermediate flow}\\ G(y)& =(N(y),A(y))\text{ (graph corresponding to flow y)}\\ A(y)& =\{(i,j)\in A\mid y_{ij}>0\}\text{ (arcs with positive flow in y)}\\ N(y)& =\{i\mid (i,j)\in A(y)\text{ or }(j,i)\in A(y)\}\text{ (nodes incident to arcs in A(y))}\\ \mathcal{S}& =\{i\mid b(i)>0\}\text{ (supply nodes)}\\ \mathcal{D}& =\{i\mid b(i)<0\}\text{ (demand nodes)}\\ \text{for P∈P},\Delta (P)& =\min \{b(s),-b(t),\min \{y_{ij}\mid (i,j)\in P\}\}\text{ (capacity of path)}\\ \text{for W∈W},\Delta (W)& =\min \{y_{ij}\mid (i,j)\in P\}\text{ (capacity of cycle)}\end{array}$$

The algorithm is outlined below:

Algorithm 4 Flow decomposition algorithm

procedure FlowDecomposition($G=(N,A),~x$)

$y:=x$

$\mathcal{P} := \emptyset$

$\mathcal{W} := \emptyset$

while $y\ne0$ do

$s:=$Select$(y)$

Do DFS starting at node $s$ until finding a cycle $W$ in $G(y)$ or a path $P$ in $G(y)$ from node $s$ to node $t\in D$

if cycle $W$ is found then

add $W$ to $\mathcal{W}$

$f(W) := \Delta(W)$

$y_{ij} := y_{ij}-\Delta(W),~\forall (i,j)\in W$

update $A(y)$ and $N(y)$

end if

if path $P$ is found then

add $P$ to $\mathcal{P}$

$f(P) := \Delta(P)$

$y_{ij} := y_{ij} - \Delta(P),~\forall (i,j)\in P$

$b(s) = b(s) - \Delta(P)$ where $s$ is the starting node of $P$

$b(t) = b(t) + \Delta(P)$ where $t$ is the ending node of $P$

update $A(y)$, $N(y)$, $\mathcal(S)$ and $\mathcal{D}$

end if

end while

end procedure

function Select(y)

if $S\ne\empty$ then

return $x\in S$

else

return $x\in N(y)$

end if

end function