2025-03-28

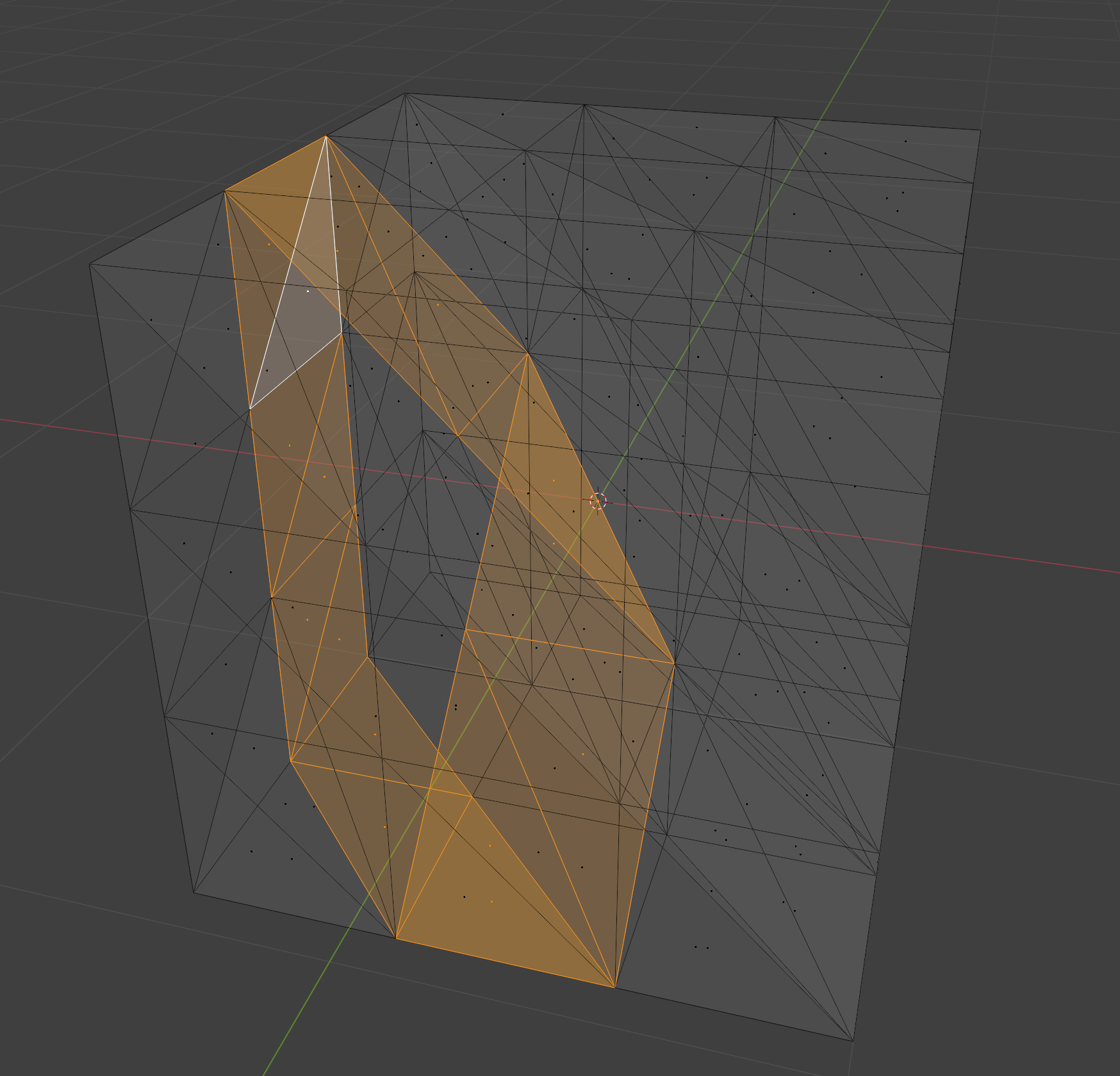
Mesh construction process:

1. Start with corner points of a cube.
2. Generate Delaunay tetrahedralization via tetgen.
3. Take the 2-skeleton
4. Subdivide twice

The resulting complex has a Mobius strip as a subcomplex:

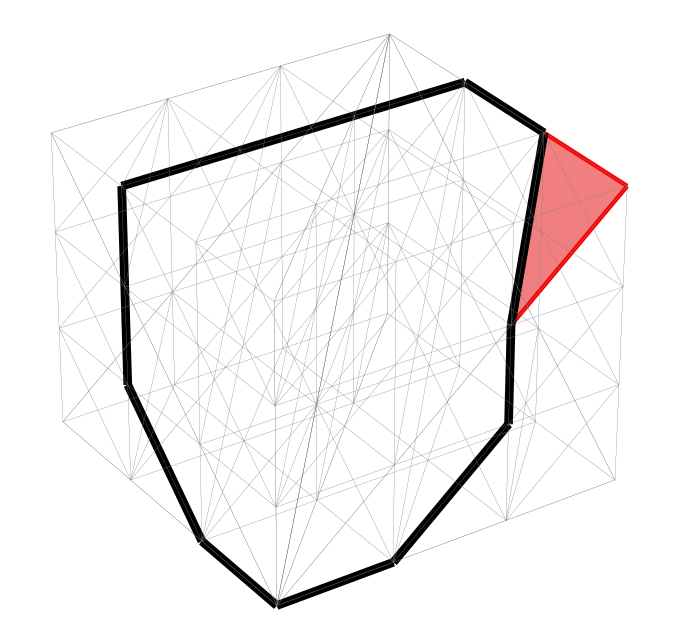
The 2-dimensional boundary matrix for the above mesh is $219\times 162$ in size. It contains the $13\times 13$ submatrix

$$\left[\begin{array}{ccccccccccccc}1& 1& & & & & & & & & & & \\ & & 1& 1& & & & & & & & & \\ & & & 1& -1& & & & & & & & \\ & & -1& & & 1& & & & & & & \\ & & & & & 1& 1& & & & & & \\ & & & & & & 1& -1& & & & & \\ & & & & & & & 1& 1& & & & \\ 1& & & & 1& & & & & & & & \\ & & & & & & & & & -1& 1& & \\ & & & & & & & & -1& & -1& & \\ & & & & & & & & & 1& & 1& \\ & 1& & & & & & & & & & & 1\\ & & & & & & & & & & & -1& -1\end{array}\right]$$

which has absolute determinant 2.

Therefore, the boundary matrix is not TU. As a result, we are guaranteed that the polyhedra corresponding to our LP has at least one non-integral corner point. However, upon solving the LP we still get integral solutions for free:

From Bala’s paper Optimal Homologous Cycles, Total Unimodularity, and Linear Programming:

Thm

$[{\partial }_2]$ is totally unimodular if and only if the simplicial complex $K$ has no Mobius subcomplex of dimension 2.

Goal: Understand why this result is true; primarily the $\Leftarrow$ direction.

Our Problem: Under what conditions (if any) are we guaranteed integral solutions?